|
Repères cartésien : 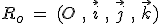
C'est la dérivée par rapport au temps du vecteur vitesse : 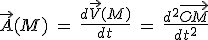 . Il représente l'accélération instantanée du mobile à l'instant t où on le calcule. . Il représente l'accélération instantanée du mobile à l'instant t où on le calcule.
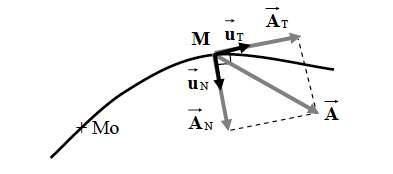
Le vecteur vitesse étant tangent à la trajectoire, le vecteur accélération, qui est sa dérivée, aura deux composantes, soit 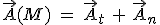 avec : avec :
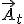 accélération tangentielle portée par la tangente en accélération tangentielle portée par la tangente en 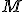 (comme la vitesse) (comme la vitesse)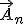 accélération normale perpendiculaire en accélération normale perpendiculaire en 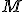 à à 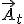 , et toujours dirigée vers la partie concave de la trajectoire (vers le centre de courbure, càd vers "l'intérieur" de la courbe) , et toujours dirigée vers la partie concave de la trajectoire (vers le centre de courbure, càd vers "l'intérieur" de la courbe)
On peut noter que l'accélération normale n'existe (est non nulle) que si la trajectoire présente une courbure.
Si 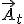 et et 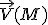 sont de même sens, le mouvement est dit accéléré (la vitesse V augmente). sont de même sens, le mouvement est dit accéléré (la vitesse V augmente).
Si 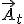 et et 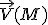 sont de sens contraires, le mouvement est dit décéléré ou ralenti (la vitesse V diminue). sont de sens contraires, le mouvement est dit décéléré ou ralenti (la vitesse V diminue).
• Coordonnées cartésiennes 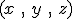
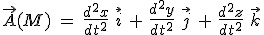
On pourra aussi écrire :
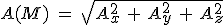 est le module du vecteur accélération, c'est une grandeur scalaire (nombre) positive qui représente la mesure de l'accélération instantanée (en m/s²). est le module du vecteur accélération, c'est une grandeur scalaire (nombre) positive qui représente la mesure de l'accélération instantanée (en m/s²).
• Coordonnées polaires 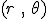
En dérivant le vecteur vitesse exprimé en polaires, et en remarquant que 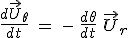 . .
On obtient 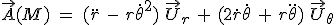 . .
Repère intrinsèque (Frenet) : 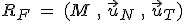
Les vecteurs du repère de Frenet étant portés par la normale et la tangente à la trajectoire, on a donc 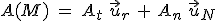 avec avec 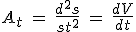 et et 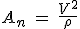 où où 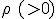 est le rayon de courbure de la trajectoire. On remarquera que est le rayon de courbure de la trajectoire. On remarquera que 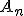 est toujours positif, donc on retrouve bien le fait que l'accélération normale est toujours dirigée vers le centre de la trajectoire. est toujours positif, donc on retrouve bien le fait que l'accélération normale est toujours dirigée vers le centre de la trajectoire.
Cas particulier : Si la trajectoire du point 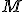 est un cercle de rayon R, alors ρ est le rayon du cercle ρ = R. Par rapport au repère polaire, on a est un cercle de rayon R, alors ρ est le rayon du cercle ρ = R. Par rapport au repère polaire, on a 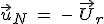 et et 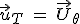 . On a donc . On a donc 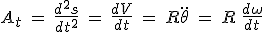 et et 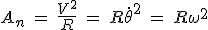 avec avec 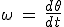 la vitesse angulaire et la vitesse angulaire et 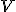 la vitesse linéaire du point la vitesse linéaire du point 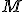 . .
Si de plus, le cercle est parcouru par le point 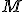 à la vitesse angulaire ω = constante (mouvement circulaire uniforme) alors l'accélération devient purement normale : à la vitesse angulaire ω = constante (mouvement circulaire uniforme) alors l'accélération devient purement normale : 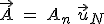 (on dit qu'elle est centripète). (on dit qu'elle est centripète).
|
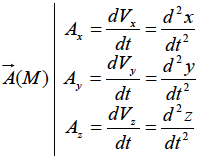
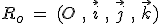
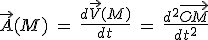 . Il représente l'accélération instantanée du mobile à l'instant t où on le calcule.
. Il représente l'accélération instantanée du mobile à l'instant t où on le calcule.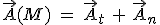 avec :
avec :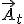 accélération tangentielle portée par la tangente en
accélération tangentielle portée par la tangente en 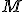 (comme la vitesse)
(comme la vitesse)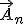 accélération normale perpendiculaire en
accélération normale perpendiculaire en 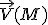 sont de même sens, le mouvement est dit accéléré (la vitesse V augmente).
sont de même sens, le mouvement est dit accéléré (la vitesse V augmente).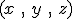
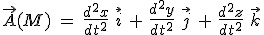
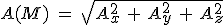 est le module du vecteur accélération, c'est une grandeur
est le module du vecteur accélération, c'est une grandeur 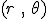
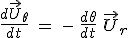 .
.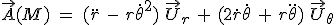 .
.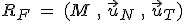
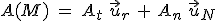 avec
avec 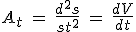 et
et 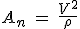 où
où 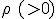 est le
est le 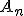 est toujours positif, donc on retrouve bien le fait que l'accélération normale est toujours dirigée vers le centre de la trajectoire.
est toujours positif, donc on retrouve bien le fait que l'accélération normale est toujours dirigée vers le centre de la trajectoire. 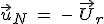 et
et 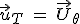 . On a donc
. On a donc 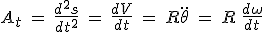 et
et 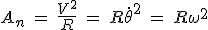 avec
avec 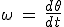 la vitesse angulaire et
la vitesse angulaire et 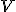 la vitesse linéaire du point
la vitesse linéaire du point 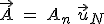 (on dit qu'elle est centripète).
(on dit qu'elle est centripète).