|
Repères cartésien : 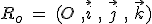
C'est la dérivée par rapport au temps du vecteur position : 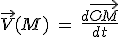 . C'est un vecteur qui est toujours tangent à la trajectoire au point . C'est un vecteur qui est toujours tangent à la trajectoire au point 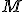 où on le calcule. Il représente la vitesse instantanée du mobile à l'instant où on le calcule. Il représente la vitesse instantanée du mobile à l'instant 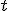 où on le calcule. où on le calcule.
• Coordonnées cartésiennes 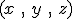
Si le vecteur position s'écrit 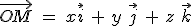 , le vecteur vitesse s'écrira , le vecteur vitesse s'écrira 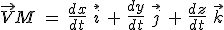 puisque les vecteurs puisque les vecteurs 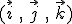 sont fixes (dérivée nulle par rapport au temps). sont fixes (dérivée nulle par rapport au temps).
On écrira également :
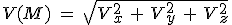 est le module du vecteur vitesse, c'est une grandeur scalaire (nombre) positive, qui représente la mesure de la vitesse du mobile (en m/s). est le module du vecteur vitesse, c'est une grandeur scalaire (nombre) positive, qui représente la mesure de la vitesse du mobile (en m/s).
• Coordonnées polaires 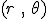
Cette fois, le vecteur position s'écrit 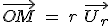 mais le vecteur mais le vecteur 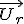 dépend du temps, puisqu'il bouge avec le point M. On aura alors dépend du temps, puisqu'il bouge avec le point M. On aura alors 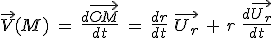 . .
On peut montrer facilement que 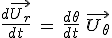 ce qui donne donc ce qui donne donc 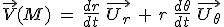 . .
On a également l'habitude de noter les dérivées par rapport au temps par un point au dessus de la grandeur : 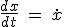 . .
On écrira donc finalement : 
Repère intrinsèque (Frenet) : 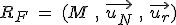
La mesure algébrique (avec signe) de la vitesse instantanée du mobile (en m/s) vaut : 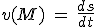 . .
Le vecteur vitesse étant tangent à la trajectoire au point 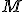 , il est donc porté par le vecteur , il est donc porté par le vecteur 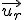 , et s'écrira : , et s'écrira : 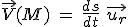
Cas particulier :
Si la trajectoire du point 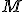 est un cercle de rayon R centré en est un cercle de rayon R centré en 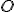 ( (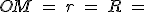 constante), le vecteur vitesse s'écrira constante), le vecteur vitesse s'écrira 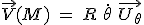 en coordonnées polaires, où le vecteur en coordonnées polaires, où le vecteur 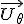 est tangent au cercle, et est donc le même que le vecteur est tangent au cercle, et est donc le même que le vecteur 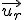 de Frenet. On aura donc de Frenet. On aura donc 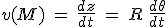 , d'où on en déduit , d'où on en déduit 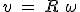 où v est la vitesse "linéaire" (en m/s) du point où v est la vitesse "linéaire" (en m/s) du point 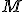 sur le cercle de rayon R, et sur le cercle de rayon R, et 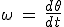 sa vitesse "angulaire" (en rad/s) (dérivée de sa "position" angulaire sa vitesse "angulaire" (en rad/s) (dérivée de sa "position" angulaire 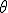 ). ).
|
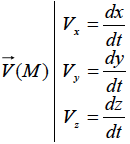
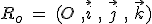
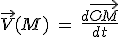 . C'est un vecteur qui est toujours tangent à la trajectoire au point
. C'est un vecteur qui est toujours tangent à la trajectoire au point 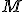 où on le calcule. Il représente la vitesse instantanée du mobile à l'instant
où on le calcule. Il représente la vitesse instantanée du mobile à l'instant 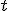 où on le calcule.
où on le calcule.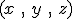
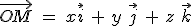 , le vecteur vitesse s'écrira
, le vecteur vitesse s'écrira 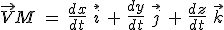 puisque les vecteurs
puisque les vecteurs 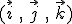 sont fixes (dérivée nulle par rapport au temps).
sont fixes (dérivée nulle par rapport au temps).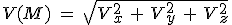 est le
est le 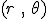
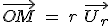 mais le vecteur
mais le vecteur 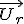 dépend du temps, puisqu'il bouge avec le point M. On aura alors
dépend du temps, puisqu'il bouge avec le point M. On aura alors 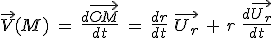 .
.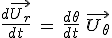 ce qui donne donc
ce qui donne donc 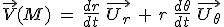 .
.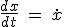 .
.
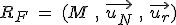
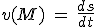 .
.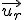 , et s'écrira :
, et s'écrira : 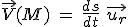
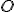 (
(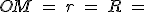 constante), le vecteur vitesse s'écrira
constante), le vecteur vitesse s'écrira 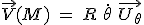 en coordonnées polaires, où le vecteur
en coordonnées polaires, où le vecteur 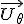 est tangent au cercle, et est donc le même que le vecteur
est tangent au cercle, et est donc le même que le vecteur 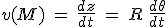 , d'où on en déduit
, d'où on en déduit 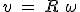 où v est la vitesse "linéaire" (en m/s) du point
où v est la vitesse "linéaire" (en m/s) du point 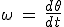 sa vitesse "angulaire" (en rad/s) (dérivée de sa "position" angulaire
sa vitesse "angulaire" (en rad/s) (dérivée de sa "position" angulaire 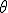 ).
).