1.4.7.6 Transfert d'inertie

Dans les calculs de motorisations en régime transitoire, il est souvent utile (voire nécessaire !) de ramener sur l'arbre moteur (en entrée) toutes les inerties et tous les couples résistants présents dans le système, et d'utiliser alors dans les calculs leurs valeurs équivalentes "vu depuis l'arbre moteur".
On a déjà établi ce qui se passe pour les couples (voir précédemment), mais comment sont "ramenées" sur l'arbre moteur les inerties présentes du côté de la charge ?
Une charge qui présente un moment d'inertie J_ch et qui tourne à la vitesse ω_ch développe un couple résistant . Si cette charge est entraînée par un moteur qui tourne à la vitesse ω_m, via un réducteur de rapport de réduction 1/N et de rendement η, alors, du côté moteur, le couple "ramené" vu par le moteur sera égal à :

Le moment d'inertie J_ch présent du côté charge est donc équivalent du côté moteur à

Conclusion : Dans un réducteur parfait, les moments d'inertie présents du côté charge sont divisés par N² quand ils sont ramenés du côté moteur.

Exemple : Considérons la chaîne cinématique suivante, dans laquelle les rapports de réduction des réducteurs de vitesse sont notés 1/N et leurs rendements η. Les différents moments d'inertie sont notés J, les vitesses de rotation ω et les couples C.

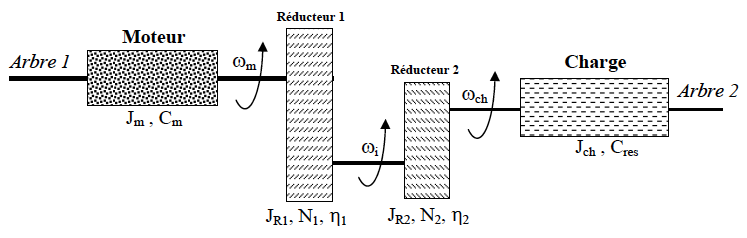
Déterminons le système équivalent "vu côté moteur" c'est-à-dire sur l'arbre 1. Pour cela il faut utiliser les relations qui sont imposées par la présence des deux réducteurs :

• pour les vitesses : et d'où

• pour le couple résistant équivalent ramené du côté moteur :

• pour le moment d'inertie total équivalent ramené du côté moteur :

Pour étudier la dynamique de ce système, il suffira alors d'écrire le principe fondamental de la dynamique "côté moteur", en utilisant les grandeurs équivalentes ramenées côté moteur pour les différentes inerties et pour le couple résistant développé par la charge, soit :