1.4.2 Travail (W)
|
Travail élémentaire ΔW d'une force Le travail élémentaire ΔW d'une force
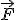 dont le point d'application effectue un "petit" déplacement de A à A' (on notera dont le point d'application effectue un "petit" déplacement de A à A' (on notera  ) sur lequel la force ne varie pas, est égal au produit scalaire de ) sur lequel la force ne varie pas, est égal au produit scalaire de 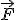 par 'lΔ : par 'lΔ : |
 |
|
Le travail (qui est une énergie) est donc une quantité scalaire (nombre) qui s'exprime en joules (J), lorsque la force est exprimée en newtons (N) et le déplacement en mètres (m).
Travail d'une force constante ou invariable Si la force reste invariable (module, direction, sens) pendant tout le déplacement, d'un point A en un point B (déplacement qui n'est plus "élémentaire"), son travail pendant ce déplacement s'écrit :
Démonstration : Il suffit de diviser la trajet AB en une infinité de "petits" déplacements élémentaires :
 Le travail s'exprime alors par la somme des travaux élémentaires correspondants :
Exemple important : travail de la force de pesanteur (vecteur poids)

Quel que soit le trajet suivi, le travail de la force de pesanteur ne dépend que de la dénivellation h entre le point de départ et le point d'arrivée :
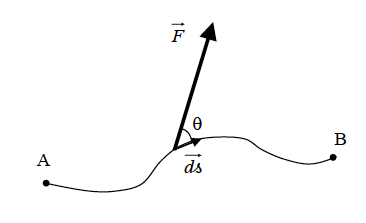
Cas général
Si la force varie le long du trajet de A en B, il faut décomposer le travail total W en petits travaux "élémentaires" dW en utilisant l'abscisse curviligne s le long de ce trajet, elle-même décomposée en petits déplacements élémentaires  : : |
 |
 |
|
Travail d'un couple Le travail élémentaire  Lorsque le couple C est constant, par les mêmes raisonnements que précédemment, le travail lors d'une rotation d'un angle 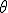 (non élémentaire) s'écrit : (non élémentaire) s'écrit : 
Exemple : Un moteur, tournant à 1500 tr.min-1, et qui exerce un couple constant de 20 N.m sur la charge qu'il entraîne, fournira en une minute un travail W = 20.(1500.2 |
 ↔
↔  ° : la force est "
° : la force est " ↔
↔  ° : la force est
° : la force est  °
°  ° : la force est "
° : la force est " fourni par un couple C lors d'une rotation élémentaire
fourni par un couple C lors d'une rotation élémentaire  vaut :
vaut : ) = 188,5 kJ.
) = 188,5 kJ.