1.2.2.2 Vecteur moment d'une force par rapport à un point

|
Pour l'étude de systèmes dans l'espace, la notion de moment scalaire ne suffit plus, et on doit le définir autrement, à partir d'un produit vectoriel
|
|
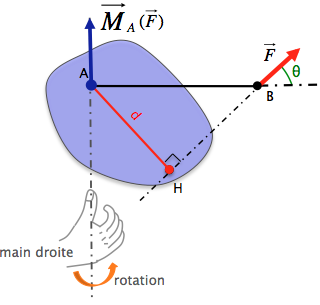
Le vecteur moment de la force 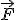 par rapport au point A est défini par par rapport au point A est défini par  où B est un point quelconque de la ligne d'action de la force où B est un point quelconque de la ligne d'action de la force 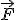 . .
De par les propriétés du produit vectoriel, le vecteur moment est perpendiculaire à la fois à la force 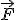 et au vecteur et au vecteur  . .
Son sens est donné par la règle des trois doigts (de la main droite) :
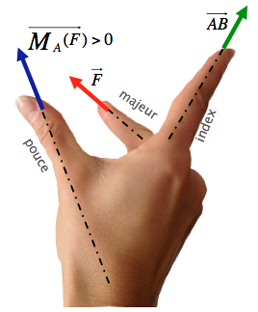
|
|
|
Remarque :  donc le moment scalaire est égal au module du moment vecteur, avec le signe résultant de la convention énoncée ci-dessus selon le sens de rotation induit par la force donc le moment scalaire est égal au module du moment vecteur, avec le signe résultant de la convention énoncée ci-dessus selon le sens de rotation induit par la force 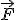 autour du point A. autour du point A.
RAPPEL : calcul du produit vectoriel en coordonnées cartésiennes
Méthode pratique : On recopie les deux premières lignes des coordonnées de 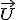 et et 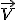 sous les deux vecteurs. La 1° ligne du produit vectoriel s'obtient alors en barrant la 1° ligne de ces coordonnées, et en calculant le déterminant des deux lignes en dessous (lignes 2 et 3). Puis on recommence en barrant la 2° ligne, et enfin la 3° ligne. sous les deux vecteurs. La 1° ligne du produit vectoriel s'obtient alors en barrant la 1° ligne de ces coordonnées, et en calculant le déterminant des deux lignes en dessous (lignes 2 et 3). Puis on recommence en barrant la 2° ligne, et enfin la 3° ligne.
Cas particulier : Si le point A appartient à l'axe de rotation du solide, alors le vecteur moment en A d'une force 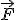 produisant ce mouvement de rotation, est porté par l'axe de rotation, et son sens sur cet axe est donné par la règle du tire-bouchon par rapport au sens de rotation du solide. produisant ce mouvement de rotation, est porté par l'axe de rotation, et son sens sur cet axe est donné par la règle du tire-bouchon par rapport au sens de rotation du solide.
|
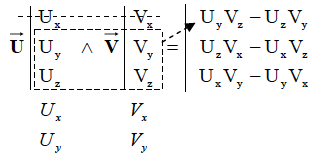
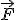 par rapport au point A est défini par
par rapport au point A est défini par  où B est un point
où B est un point  .
.
 donc le moment scalaire est égal au module du moment vecteur, avec le signe résultant de la convention énoncée ci-dessus selon le sens de rotation induit par la force
donc le moment scalaire est égal au module du moment vecteur, avec le signe résultant de la convention énoncée ci-dessus selon le sens de rotation induit par la force 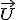 et
et 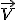 sous les deux vecteurs. La 1° ligne du produit vectoriel s'obtient alors en barrant la 1° ligne de ces coordonnées, et en calculant le déterminant des deux lignes en dessous (lignes 2 et 3). Puis on recommence en barrant la 2° ligne, et enfin la 3° ligne.
sous les deux vecteurs. La 1° ligne du produit vectoriel s'obtient alors en barrant la 1° ligne de ces coordonnées, et en calculant le déterminant des deux lignes en dessous (lignes 2 et 3). Puis on recommence en barrant la 2° ligne, et enfin la 3° ligne.