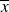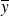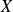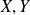Coefficient de détermination
On vient de voir que, quel que soit le nuage de points fourni (et donc quels que soient les caractères étudiés), on est toujours capable de trouver la droite la plus "proche" possible du nuage. Pour cela, on a cherché l'ordonnée à l'origine
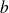et le coefficient directeur
qui minimisent l'écart quadratique moyen
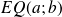entre les points du nuage et la droite d'équation
.
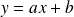Si cette valeur minimale de
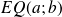(qu'on notera
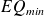) est faible, cela signifie que les points du nuage sont tous proches de la droite de régression, et donc on peut considérer qu'ils sont "approximativement" alignés, c'est-à-dire encore que l'hypothèse d'une dépendance affine de
par rapport à
semble confortée par les données recueillies.
Au contraire, si
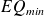est élevé, cela signifie que certains points du nuage sont éloignés de la droite de régression, et donc on peut difficilement considérer que seules les incertitudes de mesure impliquent qu'on n'ait pas obtenu des points alignés. Dans ce cas-là, les données recueillies tendent à exclure l'hypothèse d'une dépendance affine entre les caractères
et
.
Or, on a vu que l'écart quadratique moyen
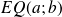est minimal quand :
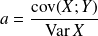et
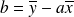
Pour ces valeurs-là, on montre (détails en cliquant ici) que :
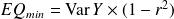avec
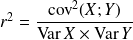
Définition :
Le coefficient
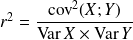est appelé coefficient de détermination : c'est un nombre toujours compris entre 0 et 1.
Par conséquent,
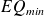est compris entre 0 et Var
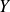. Plus particulièrement :
Quand
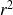est proche de 1, alors
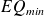est proche de 0. Dans ce cas-là, les points du nuage sont tous très proches de la droite
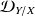.Au contraire, quand
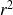est proche de 0, alors
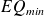est élevé comparativement à la variance de
. Dans ce cas-là, on considère que la dispersion des
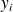(mesurée par la variance de
) n'est pas directement liée à la dispersion des
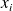. Autrement dit, il semble alors peu probable que
dépende de
selon une relation affine.
En pratique, on trouve plusieurs critères explicitant quand est-ce que
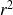est "proche" de 0 ou de 1. Nous retiendrons dans ce cours le critère suivant :
Fondamental :
On conclura en faveur d'une dépendance affine de
par rapport à
quand le coefficient de détermination
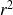est supérieur ou égal à
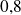. Dans le cas contraire, on préférera rejeter l'hypothèse d'une telle dépendance affine.
Remarque :
Signalons enfin que le coefficient
est, lui, appelé coefficient de corrélation de
et de
. C'est un nombre compris entre
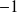et 1, du signe du coefficient directeur
de la droite de régression
.
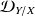Exemple : Exemple basique - Partie 4
On travaille toujours avec les données suivantes :
On a trouvé jusqu'à présent :
Grandeurs |
|
| Var
| cov(
|
|
|
Valeurs | 10.375 | 11.125 | 6.734375 | 8.203125 | 1.218 | -1.513 |
Pour conclure quant à une éventuelle dépendance affine de
en
, on calcule tout d'abord la variance de
:
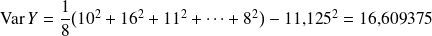
Puis le coefficient de détermination :
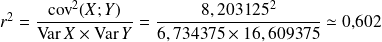
Ce coefficient est inférieur à 0.8, donc on conclut que les données étudiées tendent à exclure l'hypothèse de dépendance affine de
par rapport à
.
