Principe de la résolution mathématique
Pour trouver la droite de régression au sens des moindres carrés, il faut trouver les valeurs de
et
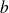qui rendent minimal l'écart quadratique moyen :
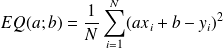
Il s'agit donc de trouver le minimum d'une fonction de 2 variables.
Rappel :
On rappelle que, si une fonction
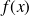d'une seule variable dérivable sur un intervalle ouvert
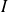admet un extremum en
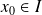, alors
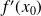est nul. Ce théorème admet une généralisation au cas des fonctions de plusieurs variables : si une fonction
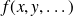(différentiable sur un ouvert) admet un extremum en
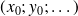, alors toutes les dérivées partielles de
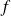sont nulles en
.
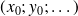Ainsi, on obtient l'ordonnée à l'origine
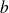et le coefficient directeur
de la droite de régression de
en
en résolvant le système donné par :
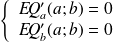
Le lecteur curieux (et motivé) trouvera les détails de la résolution de ce système en cliquant ici.
On montre que, à condition que les points du nuage n'aient pas tous la même abscisse, le système admet une solution unique pour
et pour
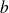. On trouve dans un premier temps :
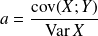avec
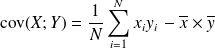
Définition : Covariance
On appelle covariance de
et de
le nombre cov
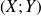défini par
.
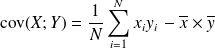On peut exprimer la covariance par l'intermédiaire d'une autre formule consultable en cliquant ici.
Dans un deuxième temps, on en déduit :
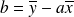avec
trouvé précédemment
Cette dernière formule implique que les coordonnées du point moyen
du nuage vérifient l'équation de la droite de régression.
Remarque :
La droite de régression linéaire de
en
au sens des moindres carrés passe toujours par le point moyen du nuage.
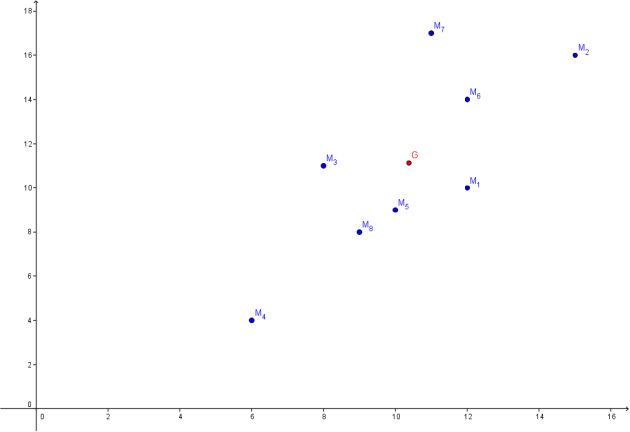
Exemple : Exemple basique - Partie 3
Reprenons les données et le nuage de points de l'exemple basique introduit précédemment :
D'après ce qui précède, pour déterminer le coefficient directeur
et l'ordonnée à l'origine
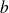de la droite de régression linéaire de
en
, il faut calculer la covariance de
et
, la variance de
et les moyennes de
et de
. Ces 2 dernières valeurs ont déjà été trouvées (
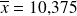et
).
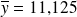Calculons alors la variance de
:
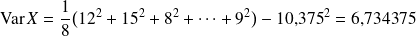
Puis la covariance de
et
:
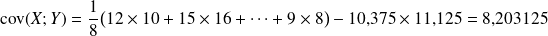
On peut alors en déduire les coefficients
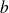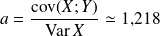et
:
et
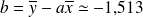
Finalement, on a :
.
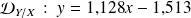