Écart quadratique moyen
Les résidus vus précédemment peuvent être aussi bien négatifs que positifs : si on calcule la moyenne des résidus associés à un nuage
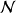de points et à une droite
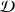, on peut alors obtenir, par des effets de compensation "+/-", un résultat très proche de zéro même si les points du nuage sont tous très éloignés de la droite
.
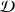Pour éviter ce phénomène de compensation, on utilise les carrés des résidus. En effet, si la moyenne des carrés des résidus associés à un nuage et une droite est faible, cela signifie que tous les résidus sont faibles (en valeur absolue) et donc que les points du nuage sont "proches" de la droite. On peut alors, en comparant les moyennes obtenues pour deux droites
et
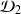, déterminer laquelle des deux droites "convient" mieux pour un nuage de points donné.
Définition :
On appelle écart quadratique moyen du nuage
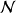par rapport à la droite
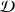la moyenne des carrés des résidus.
Fondamental :
Les points d'un nuage sont plus proches d'une droite
que d'une droite
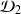si l'écart quadratique moyen par rapport à
est plus petit que l'écart quadratique moyen par rapport à
.
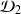Plus précisément, dans un repère orthonormé, on considère un nuage de points
,
, ... ,
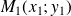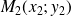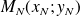, et une droite
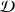d'équation
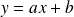. On note
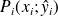, pour
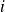allant de 1 à
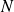, le point de
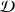ayant la même abscisse que
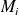. Ses coordonnées vérifient l'équation de
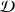, donc
.
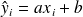Pour ce nuage de points fixé, l'écart quadratique des points du nuage par rapport à la droite
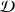ne dépend que du coefficient directeur
et de l'ordonnée à l'origine
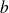, et s'écrit
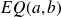avec :
