Lorsqu’il est nécessaire de passer à des éléments de taille supérieure, la façon dont le problème a été traité peut aider à la mise en œuvre. Ainsi le problème précédent peut être réutilisé pour réaliser un additionneur 4 bits.

Quelle que soit la réalisation de l’additionneur 1 bit, on peut envisager d’étendre par instanciation de modules précédents. On doit disposer de 4 modules 1 bit que l’on devra interconnecter pour réaliser un additionneur 4 bits :

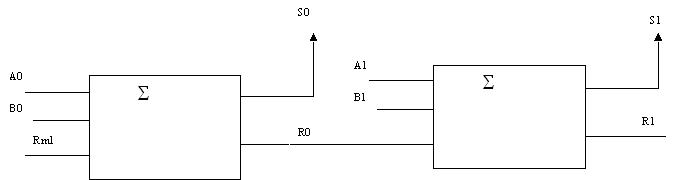
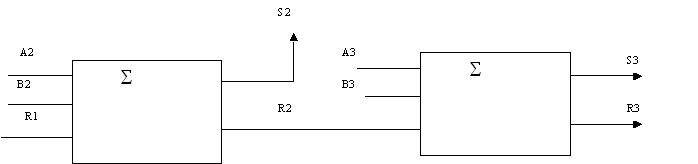
Le programme sera :

module ADD4Bit (A, B, Rm1, S, R3) ;

input [3 :0] A, B ;

input Rm1 ;

output [3 :0] S ;

output R3 ;

wire R0, R1, R2 ;

Add1Bit Add0(A[0], B[0], Rm1, S[0], R0) ;

Add1Bit Add1(A[1], B[1], R0, S[1], R1) ;

Add1Bit Add2(A[2], B[2], R1, S[2], R2) ;

Add1Bit Add3(A[3], B[3], R2, S[3], R3) ;

endmodule

Remarque : cette solution permet tout, mais il faudra écrire chacun des modules, l'extension n'est pas modulaire.

Est-il envisageable de traiter le cas de l’additionneur 4 bits par une autre analyse ? Réponse : OUI !

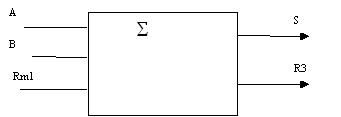
La méthode consistant à traiter le problème par l’arithmétique est très facile à étendre à 4 bits, voire à n bits. Seule la déclaration de bus pour A, B et S est différente. La version 4 bits est la suivante :

module ADD4Bit (A, B, Rm1, S, R3) ;

input [3 :0] A, B ;

input R0 ;

output [3 :0] S ;

output R3 ;

assign {R3, S} = A + B + Rm1 + 0 ;

endmodule

Le cas d'un additionneur n bits est donné ci-dessous avec n= 18 :

parameter n = 18;

module ADDnBit (A, B, Rm1, S, Rn) ;

input [n :0] A, B ;

input R0 ;

output [n :0] S ;

output Rn ;

assign {Rn, S} = A + B + R0 + 0 ;

endmodule

Le contrôle de la taille de la valeur 0 aurait été un problème à l'extension de ce module.

La taille pour les extensions est limitée aux 32 bits de calcul.