C'est un critère de réglage très facile à mettre en œuvre et qui donne de bons résultats. Il ne peut être utilisé que pour le réglage d'un correcteur P.I., P.D. ou P.I.D.
Afin de privilégier la qualité amortissement de l'asservissement, nous proposerons des réglages différents que ceux que préconisaient Ziegler et Nichols (notamment une action proportionnelle K plus faible). Ainsi nous appliquerons le critère de Z.N.M. (M comme modifié).
L'avantage incontestable de ce critère de réglage est qu'il peut s'appliquer aussi bien sur le modèle théorique qu'expérimentalement sur l'asservissement réalisé.
La démarche est simple: déterminer les conditions du régime critique de la boucle non corrigée (avec uniquement le réglage d'un gain K): voir le paragraphe 6.2.5.
Nous obtenons deux valeurs: wc et Kc.
wc est la pulsation de la sinusoïde engendrée par la boucle « juste instable ».
On en déduit la période de cette sinusoïde: Tc = 2p / wc.
Si nous faisons l'étude expérimentale du régime critique de la boucle non corrigée, après avoir trouvé le réglage critique Kc qui rend la boucle juste instable, nous mesurons directement la période Tc de la sinusoïde engendrée.
Les réglages de Z.N.M. sont les suivants:
Type de correcteur -->
Paramètres réglables |
P. |
P.I. |
P.D. |
P.I.D série |
P.I.D parallèle |
K (valeurs indicatives) |
0,2Kc |
0,25Kc |
0,35Kc |
0,18Kc |
0,3Kc |
Ti |
|
0,9Tc |
|
0,3Tc |
0,5Tc |
Td |
|
|
0,2Tc |
0,2Tc |
0,12Tc |
|
La fonction de transfert du correcteur P.I.D. série est:
R(p) = K[1 + 1/Tip][1 + Tdp/(1 + 0,1Tdp)]
La fonction de transfert du correcteur P.I.D. parallèle est:
R(p) = K[1 + 1/Tip + Tdp/(1 + 0,1Tdp)]
Les valeurs de Ti et de Td étant données, on doit ajuster l'action proportionnelle K pour obtenir un amortissement satisfaisant.
Les valeurs de K données dans le tableau sont donc indicatives.
En fonction du système asservi on peut être amené à augmenter ou diminuer ce gain pour obtenir par exemple, par la théorie, une marge de phase donnée, ou expérimentalement, un dépassement donné de la réponse indicielle.
| 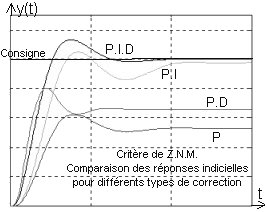 |
Les réponses indicielles ci-contre permettent de comparer, sur un exemple, les performances d'un asservissement en classe 0 sans correction (P), puis avec correction P.D., et en classe 1, correction P.I. puis correction P.I.D.
Les quatre réponses étant bien amorties, on peut comparer les qualités précision et vélocité:
Classement du plus précis au moins précis: P.I.D., P.I., P.D., P.
Classement du plus véloce au moins véloce: P.D., P.I.D., P., P.I.

