Ce correcteur ne change pas la classe de l'asservissement mais permet de remonter la courbe de gain en boucle ouverte dans le domaine des basses pulsations, ce qui diminue soit l'erreur de position en classe 0 soit l'erreur de traînage en classe 1. Mais surtout ce correcteur décale la courbe de gain en boucle ouverte vers la droite (hautes pulsations) ce qui permet une augmentation importante de la bande passante de l'asservissement, donc une amélioration sensible de la vélocité.
|
Fonction de transfert du correcteur P.D ou à avance de phase:
R(p) = K[1 + (Tdp)/(1 + tdp)] = K(1 + Tap) / (1 + b.Tap) avec b<1.
La première écriture de R(p) correspond à la fonction de transfert du correcteur P.D. et la seconde à la fonction de transfert du correcteur à avance de phase. Mais ces deux fonctions de transfert sont égales avec:
td = b.Ta et Ta = Td + td.
Nous allons travailler avec la seconde expression, qui est sous une forme canonique.
Transmittance harmonique: R(jw) = K(1 + jwTa) / (1 + jbwTa)
çR(jw)ç = [K(1 + w2Ta2)1/2] / (1 + w2b2Ta2)1/2
^R(jw) = arctan(wTa) - arctan(wbTa)
b étant inférieur à 1, l'argument est toujours positif.
Les lieux de Bode de R(jw) sont représentés ci-contre:
La courbe de phase présente un axe de symétrie pour une pulsation wM qui est la moyenne géométrique des deux pulsations 1/(Ta) au numérateur et 1/ bTa au dénominateur:
wM = 1/(Ta.b1/2) .
|
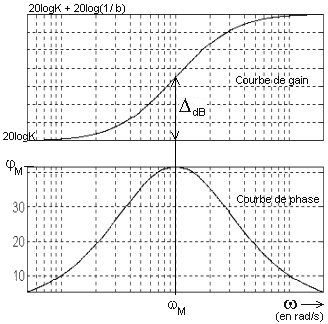 |
Pour cette pulsation l'avance de phase maximum est:
jM = arctan(b-1/2) - arctan(b1/2) = arcsin[(1-b)/(1+b)].
Pour cette pulsation wM, l'augmentation du gain par rapport à 20logK est:
DdB = 10log(1/ b) .
b | 0,5 | 0,4 | 0,3 | 0,2 | 0,1 | 0,05 |
| jM | + 19,5° | + 25,4° | + 32,6° | + 41,8° | + 54,9° | + 64,8° |
DdB | + 3 dB | + 4 dB | + 5,2 dB | + 7 dB | + 10 dB | + 13 dB |
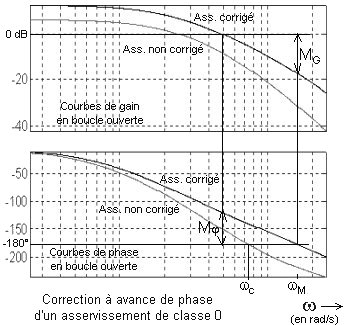
On suppose que l'asservissement non corrigé, de classe 0, est très bien amorti (par exemple avec une marge de phase de 75°) mais son erreur de position est grande et son temps de montée trop important. On souhaite réduire l'erreur de position et le temps de montée grâce au correcteur à avance de phase. Plus on choisira b faible, plus on améliorera les qualités précision et vélocité. Mais en pratique on se limite à b = 0,05.
|
Critère de réglage:
On règle b en fonction de l'objectif fixé (dans un correcteur P.D. on prend généralement b = 0,1).
Pour notre exemple nous choisissons b = 0,2 .
La pulsation centrale du correcteur est alors réglée à environ une octave à droite de la pulsation critique de l'asservissement non corrigé:
wM = wc/(1,25.b1/2) donc Ta = 1,25/wc .
Avec ces réglages les marges de stabilité seront satisfaisantes en adoptant un gain K compris entre 2 et 2,5.
Pour notre exemple nous avons pris K = 2.
Les lieux de Bode ci-contre montrent qu'avec ces réglages les objectifs décrits au paragraphe 7.1 sont atteints.
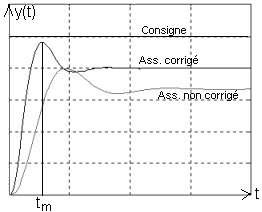
Pratiquement, en classe 0 on peut sans difficulté avec le correcteur à avance de phase diviser l'erreur de position par 2, et diviser le temps de montée par 2. On a alors un asservissement beaucoup plus performant que sans correction, nous pourrions dire « 4 fois » plus performant.
Les réponses indicielles (en boucle fermée bien entendu) sont données ci-contre:
Nous allons maintenant examiner la correction P.D. d'un asservissement de classe 1.
Critère de réglage:
b = 0,1 Td = 0,9Ta = 1,125/wc donc Td = 0,18Tc puisque Tc = 2p/wc
Rappel: wc est la pulsation critique avant correction.
|
 |
La valeur de K permettant de retrouver de bonnes marges de stabilité est alors comprise entre 2,5 et 3 (dans l'exemple présenté à la page suivante: K = 2,8).
Ainsi l'erreur de traînage de l'asservissement est divisée par K, divisée par 2,8 dans l'exemple qui suit.
Bien sûr la bande passante sera aussi sensiblement augmentée (dans un rapport de l'ordre de 2,5).
Lieux de Bode en boucle ouverte:
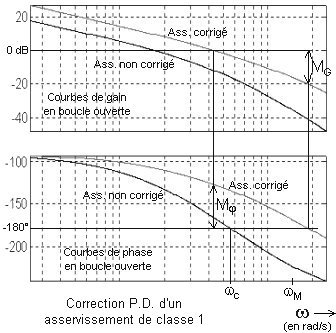 |
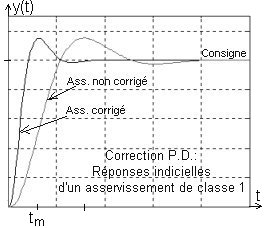
L'asservissement corrigé est 2,8 fois plus précis (erreur de traînage 2,8 fois plus petite), et environ 2,5 fois plus véloce (temps de montée divisé par 2,5). On peut dire que l'asservissement corrigé est « 7 fois » plus performant. De plus, sur les lieux de Bode en boucle ouverte, on constate que les marges de stabilité sont les mêmes avec correction que sans correction (amortissement identique de la boucle).
|

