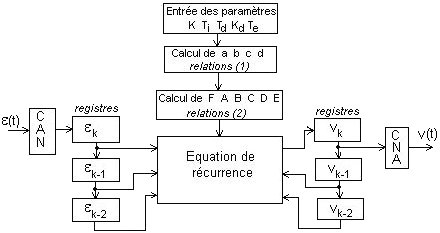
Dans ce dernier paragraphe nous allons aborder les équations de récurrence qui sont le point de départ de l'étude des systèmes échantillonnés.
Lorsqu'une fonction continue v(t) est échantillonnée, on s'intéresse à sa valeur à des instants séparés par une période d'échantillonnage T_e:   v_k-1= v(t_k-1)      v_k= v(t_k)    et    T_e= t_k - t_k-1 .
La dérivée dv(t)/dt à l'instant t_k est donc:  (dv/dt)_tk= (v_k - v_k-1) / T_e .
De même on peut exprimer la dérivée seconde:
(d²v/dt²)_tk= [(dv/dt)_tk - (dv/dt)_tk-1] / T_e = [(v_k - v_k-1) / T_e - (v_k-1 - v_k-2) / T_e] / T_e

(d²v/dt²)_tk= (v_k - 2.v_k-1 + v_k-2) / T_e² .

Application au correcteur P.I.D. de type parallèle de fonction de transfert:  R(p) = K[1 + 1/ T_ip + T_dp/(1+ T_dp/K_d)].
Cette fonction de transfert mise sous forme d'un rapport de deux polynômes est :   R(p) = (K + ap + bp²) / (cp + dp²)  avec:
relations (1):       a = K(T_i + T_d/K_d)         b = K.T_i.T_d(1 + 1/K_d)         c = T_i         d = T_i.T_d/K_d .
La fonction de transfert du correcteur est donc:   R(p) = V(p)/e(p) = (K + ap + bp²) / (cp + dp²) .
On en déduit l'équation différentielle:   d.v'' + c.v' = K.e + a.e' + b.e''
Remplaçons les dérivées par les relations vues au début du paragraphe:
d.(v_k - 2.v_k-1 + v_k-2) / T_e² + c.(v_k - v_k-1) / T_e   =   K.e_k + a.(e_k - e_k-1) / T_e + b.(e_k - 2.e_k-1 + e_k-2) / T_e²
On en déduit l'équation de récurrence qui donne v_k en fonction des 2 valeurs antérieures de v  et de e_k et des 2 valeurs antérieures de e:
  v_k   =   A.v_k-1  +  B.v_k-2  +  C.e_k  +  D.e_k-1  +  E.e_k-2     avec:
relations (2):    A = (2.d+c.T_e)/F     B = -d/F     C = (K.T_e²+a.T_e+b)/F     D = -(a.T_e+2.b)/F     E = b/F     F = (d+cT_e) .
La conception du correcteur P.I.D. programmé est donc la suivante:

Fin du cours