Contrairement à l'étude temporelle qui nécessitait une décomposition en une somme d'éléments simples de la fonction de transfert, l'étude harmonique oblige seulement à factoriser le dénominateur ainsi que le numérateur de cette fonction de transfert. Ainsi en remplaçant p par jw le nombre complexe T(jw) sera le produit de nombres complexes élémentaires.
Or le module du produit de nombres complexes est égal au produit des modules et son argument est égal à la somme des arguments.
Puisque les lieux de Bode représentent 20logçT(jw)ç ce produit des modules devient une somme.
Ainsi il suffit d'ajouter les courbes de gain de chaque facteur et d'ajouter les courbes de phase de chaque facteur pour obtenir les lieux de Bode d'un système quelconque. 
 
Remarque: La factorisation du dénominateur de la fonction de transfert correspond en remplaçant p par jw au produit de transmittances harmoniques élémentaires étudiées en détails dans les paragraphes précédents (4.4 4.5 4.6 et 4.7).
Par contre pour le numérateur on peut considérer que chaque facteur correspond à l'inverse d'une de ces transmittances harmoniques élémentaires (inverse du module et opposé de l'argument). Pour les lieux de Bode il suffit donc, pour représenter la courbe de gain et la courbe de phase d'un facteur du numérateur, de "retourner" les courbes: une diminution du gain avec une pente (-1) devient une augmentation du gain avec une pente (+1), et un retard de phase devient une avance de phase.

Exemple d'étude harmonique d'un système compliqué

L'exemple ci-dessous, à priori très compliqué, montre qu'à partir du moment où la fonction de transfert est mise sous sa forme canonique factorisée (dénominateur et numérateur) l'écriture du module et de l'argument du nombre complexe T(jw) ne pose aucune difficulté majeure, puisqu'on s'intéresse à un seul facteur à la fois. 
 

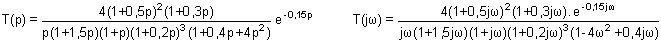
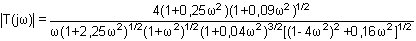
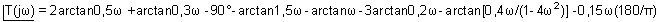
Remarques:
L'argument est exprimé en degrés d'arc de façon à "coller" à l'expérimentation (on mesure les déphasages en degrés).
Ainsi l'imaginaire pur a un argument de 90° (c.à.d. p/2 rad).
De même pour le nombre complexe e^-0,15jw (représentation polaire d'un nombre complexe), son module est égal à 1 et son argument est -0,15w rad; cet argument est converti en degrés en multipliant par 180/p.