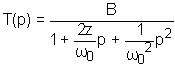
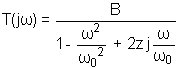
Le nombre complexe T(jw) sera étudié en détails plus loin. Les représentations de ce nombre complexe sont données ci-dessous.
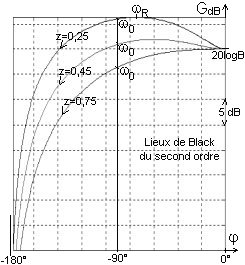
Le lieu de Nyquist est d'autant plus « enflé » que z est faible. L'intersection du lieu de Nyquist avec l'axe imaginaire (pour un argument de - 90°) se fait toujours pour une pulsation w = w0 (quelle que soit la valeur de z).
|  |
 |
 |
Le lieu de Black présente une asymptote verticale à - 180°. Pour w = w0 on a un argument de - 90° quelle que soit la valeur du coefficient d'amortissement z.
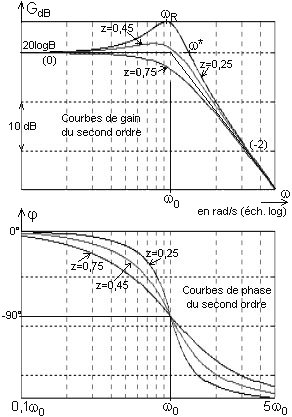
Lieux de Bode:
Le diagramme asymptotique de gain est constitué, dans le domaine des basses pulsations, d'une asymptote horizontale [pente (0)] à l'ordonnée BdB = 20logB, et à partir de
w = w0 d'une asymptote de pente (-2) c.à.d. - 40 dB/décade. Dans le domaine des hautes pulsations, le second ordre se comporte exactement comme deux intégrateurs (à partir de w = 10w0).
Plus z est faible, plus la résonance est importante.
La courbe de phase admet un centre de symétrie en w0 pour j(w0) = - 90°.
A l'asymptote de pente (0) pour le gain correspond une asymptote à 0° pour la phase.
A l'asymptote de pente (-2) pour le gain correspond une asymptote à (-2) fois 90°.
Il y a corrélation entre la pente de la courbe de gain et la valeur du déphasage.
Notamment on remarque qu'une résonance importante (pour z faible) s'accompagne d'une variation rapide du déphasage autour de w0.
|
Etude du nombre complexe T(jw):
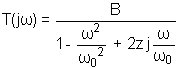
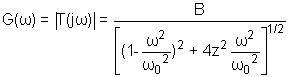
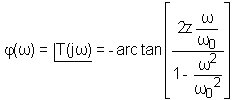
Rappels: B est le gain statique, w0 est la pulsation naturelle en rad/s, et z est le coefficient d'amortissement compris entre 0 et 1 (sans dimension).
Etude de l'argument j(w) :
La fonction j(w) varie de 0° à - 180° quand la pulsation varie de 0 à l'infini. La valeur caractéristique est - 90°.
L'expression de j(w) montre que pour w = w0 la tangente est infinie et correspond à un déphasage de - 90° et ceci quelle que soit la valeur de z : j(w0) = - 90° " z .
Déterminons maintenant la valeur des deux pulsations w1 et w2 telles que les déphasages soient respectivement de - 45° et de - 135°. On a -tan[j(w)] = 2z.x / (1 - x2) en posant x = w/w0.
Pour un argument de - 45° il faut -tan[j(w)] = 1, c.à.d. (1 - x2) = 2z.x donc : x2 + 2z.x - 1 = 0.
Seule la solution positive de cette équation du second degré nous intéresse puisque x est un rapport de deux pulsations.
On trouve x1 = (1 + z2)1/2 - z d'où w1 = w0[(1 + z2)1/2 - z] .
Pour un argument de - 135° il faut -tan[j(w)] = -1, c.à.d. (1 - x2) = -2z.x donc : x2 - 2z.x - 1 = 0.
Seule la solution positive de cette équation du second degré nous intéresse.
On trouve x2 = (1 + z2)1/2 + z d'où w2 = w0[(1 + z2)1/2 + z] .
Identification de z et w0 uniquement par des mesures de déphasage:
On règle la pulsation de la sinuso´de de commande pour obtenir en régime permanent un déphasage de - 45° puis de - 135°. On relève la valeur de chacune de ces deux pulsations particulières: w1 à - 45° et w2 à - 135°.
Les expressions ci-dessus permettent de montrer
. d'une part que w1.w2 = w02 d'où w0 = [w1.w2]1/2 (w0 est la moyenne géométrique des deux mesures),
. et d'autre part que la différence w2 - w1 = 2z.w0 est proportionnelle à z (la courbe de phase est d'autant plus pentue que z est faible).
Ainsi: w0 = [w1.w2]1/2 et z = (w2 - w1) / 2w0 .
La mesure du gain statique B se fait à une pulsation inférieure à w0/10. Un gain se mesure simplement en faisant le rapport de l'amplitude de la sinuso´de de sortie sur l'amplitude de la sinuso´de d'entrée (en pratique on mesure les amplitudes crête à crête).
Etude du module G(w) :
La fonction G(w) est plus difficile à étudier que la fonction argument.
Surtout il n'est pas possible de déterminer directement la valeur de w0 par une mesure de gain.
Par contre il peut y avoir un phénomène de résonance (maximum de gain) et les caractéristiques de cette résonance peuvent permettre d'identifier le système du second ordre.
Condition d'existence de la résonance.
Il suffit que la dérivée dG(w)/dw s'annule.
L'expression de G(w) donnÚe à la page précédente peut s'écrire:
G(w) = B[f(w)]-1/2 avec f(w) = [(1 - w2/w02)2 + 4z2(w2/w02)] Donc:
dG(w)/dw = -0,5B[f(w)]-3/2.f '(w).
dG(w)/dw = 0 si f '(w) = 0.
On pose cette fois x = w2/w02.
f(x) = (1 - x)2 + 4z2.x = x2 +2(2z2-1)x +1 d'où df(x)/dx = 2x + 2(2z2-1).
La dérivée s'annule donc pour x = w2/w02 = 1 - 2z2 c.à.d. pour w = w0(1 - 2z2)1/2.
Ainsi pour que la résonance existe il faut (1 - 2z2) positif donc z < 2-1/2 @ 0,7.
Dans ces conditions la pulsation de résonance est : wR = w0[1 - 2z2]1/2.
Que vaut alors le maximum de gain ?
Il suffit de remplacer w par wR dans l'expression de G(w) donc de remplacer x par (1 - 2z2) dans G(x).
G(x) = B[(1 - x)2 + 4z2x]-1/2.
Gmax = B[(1 -1 +2z2)2 + 4z2(1 - 2z2)]-1/2 = B[4z2 - 4z4]-1/2 = B/[2z(1-z2)1/2].
On définit un coefficient de résonance Q qui est le rapport entre le gain maximum et le gain statique: Q = Gmax/B.
Ce coefficient de résonance, facile à mesurer, ne dépendant que de z permet l'identification du coefficient d'amortissement du système.
Q = 1 / [2z(1-z2)1/2].
On peut poser z = sin a puisque z est inférieur à 0,7 quand il y a résonance. D'où Q = 1/[2sin a.cos a] = 1/(sin 2a).
Il est ainsi facile d'exprimer a = 0,5.arc sin(1/Q) donc z = sin[ 0,5.arc sin(1/Q)].
Ayant déterminé la valeur de z, l'identification de w0 pourrait se faire par la mesure de wR. Mais comme cette pulsation est définie par un maximum de gain la précision n'est pas très bonne (on peut faire varier la pulsation sans qu'on observe une variation du gain).
On préfère donc mesurer la pulsation w* telle que le gain du système retrouve la valeur du gain statique (voir courbe de gain ci-dessus).
Il faut donc résoudre G(x) = B[(1 - x)2 + 4z2x]-1/2 = B donc (1 - x)2 + 4z2x = 1 c.à.d.: x2 + 2x(2z2 - 1) = 0 ==> x[x + 2(2z2 - 1)] = 0 ==> x = 2(1 - 2z2).
Ainsi w* = w0[2(1 - 2z2)]1/2 = wR.21/2.
Après avoir identifié z par la mesure du coefficient de résonance Q, on pourra identifier w0 par la mesure de w*:
w0 = w*/ [2(1 - 2z2)]1/2
Calculons maintenant le gain du système pour une sinuso´de de commande dont la pulsation est réglée à la valeur de sa pulsation naturelle :
Dans la relation de G(w), si on remplace w par w0, on voit immédiatement les simplifications et on obtient: G(w0) = B/2z.
La méthode d'identification la plus commode et la plus simple est la suivante:
On recherche la pulsation de la sinuso´de de commande pour obtenir un déphasage de - 90°. Cette pulsation correspond à la pulsation naturelle w0 du système. On mesure alors le gain G(w0). Enfin on se place à une décade en dessous (pulsation inférieure à w0/10) et on mesure à nouveau le gain (qui sera pratiquement le gain statique B).
Les mesures de B et de w0 sont donc des mesures directes.
Il ne reste plus qu'à calculer z = B / [2G(w0)].
La fonction de transfert du système sera alors : T(p) = B/[1 + ap + bp2] avec a = 2z/w0 et b = 1/w02.

