Tout polynôme à coefficients réels peut se décomposer en produits de monômes (ordre 1) et de trinômes (ordre 2), à coefficients réels.

Ce théorème classique de mathématiques montre l'importance majeure de la bonne connaissance des propriétés des systèmes des premier et second ordre.

Le changement radical entre premier et second ordre est l'apparition possible de pôles complexes conjugués. De tels pôles peuvent conférer à un système linéaire un comportement oscillatoire (amorti, souhaitons le...).

3.3.a Amortissement ou fréquence de coupure : un compromis

La fonction de transfert (rappelons qu'il s'agit ici du produit G*H) d'un système du second ordre peut être écrite, sous la classique forme canonique qui fait intervenir une pulsation de coupure, ω₀ , et un coefficient d'amortissement m :

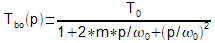
Les calculs du paragraphe 2.3.b s'appliquent évidemment sans difficulté, ils conduisent au résultat majeurs suivants :

Le produit m*ω₀ est le paramètre invariant du système.

Le coefficient d'amortissement m est divisé par  : .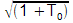

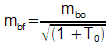La pulsation de coupure est multipliée par le même facteur : .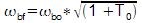

Ce résultat est d'une importance capitale : il montre qu'un système du second ordre peut devenir très largement sous amorti en boucle fermée, c'est à dire que le contrôle en boucle fermée peut conduire, dès le second ordre, à un comportement oscillatoire amorti.

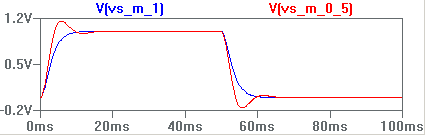
Rappelons ici qu'un amortissement convenable de la réponse transitoire d'un système suppose que le coefficient d'amortissement reste proche de 1, typiquement compris entre 0,5 et 1 :

3.3.b Lieu des pôles

Le comportement d'un système du second ordre, déterminé par ses pôles, se calcule aisément sous forme analytique. En fonction des deux paramètres canoniques w₀ et m, les pôles sont donnés par :

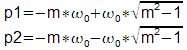
Quand le gain de boucle (T₀) augmente, le coefficient d'amortissement en boucle fermée peut devenir inférieur à 1. Les racines sont alors complexes conjuguées :

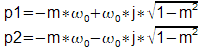
Au delà de cette valeur critique de T₀ , la partie réelle des pôles est indépendante de T₀ , seule la partie imaginaire augmente quand T₀ augmente.

Le lieu des pôles (ou lieu d'Evans) est un ensemble de courbes, dans le plan complexe des p (variable de Laplace), qui représente l'évolution des pôles quand T₀ varie.

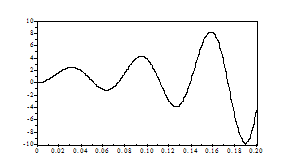
Par exemple, pour un système du second ordre ayant deux pôles réels négatifs en boucle ouverte, on obtient un lieu du style :

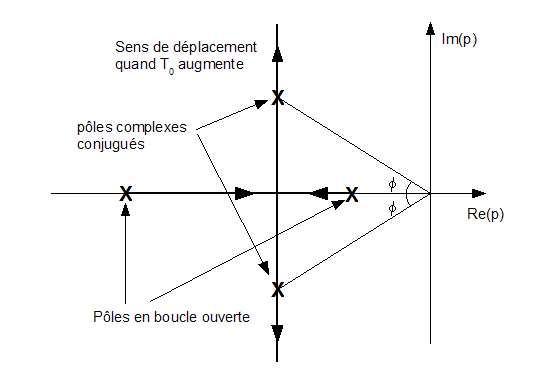
Quand |m| < 1 on peut remarquer que |m| représente le cosinus de l'angle phi fait par le rayon vecteur d'un pôle complexe et l'axe des réels (voir figure).