- Généralités sur la stabilté
Ecarter un système de sa
position d’équilibre pour conclure sur sa stabilité revient au sens théorique à
étudier la réponse impulsionnelle du système.
Pour trouver la transformée
inverse du transfert, il faut faire apparaître les éléments simples qui se
distinguent par la nature des pôles (réels
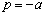
ou
complexes
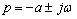
) distincts ou multiples :
et qui ont
respectivement pour transformée inverse
Pour que ces expressions tendent
vers 0 quand t tend vers l’infini, il faut que a soit
strictement positif.
Conclusion :
un
système est stable si tous ses pôles sont situés strictement dans le demi-plan
de gauche du plan complexe (
,
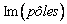), c’est le domaine de stabilité
absolue.
Pour définir un domaine de stabilité
relative, nous imposons une certaine qualité d’amortissement :
- pôles réels : forme canonique
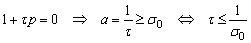
- pôles complexes : forme canonique
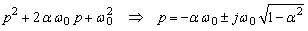les
pôles se situent alors sur des droites passant par l’origine et faisant un
angle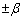 
avec l’axe des imaginaires où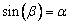 
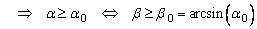
Conclusion : un système a
une stabilité pratique satisfaisante si tous ses pôles réels sont à gauche de
la droite 
et tous ses pôles complexes
dans le secteur 
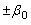du plan complexe à
partie réelle négative (voir figure ci-dessous).
L’analyse de la stabilité se fera
avec un paramètre variable k (amplification du signal d’erreur :
action proportionnelle) et un retour unitaire toujours possible en comparant
consigne (image de l’entrée) et mesure (image de la sortie).
La fonction de transfert de
boucle fermée est :
Le polynôme caractéristique
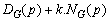
permet d’étudier la stabilité en
fonction du réglage du gain
k par la recherche de ses racines (lieu des
racines ou lieux d’Evans).
