Ce critère permet de trouver les conditions de
stabilité
absolue sans calculer les racines du polynôme caractéristique de la boucle.
- Ordonner le polynôme dans l’ordre décroissant des puissances de
p :
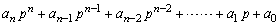
- Former le tableau de Routh : (exemple pour n impair)
Pour que la boucle soit stable, il faut que tous les
coefficients du polynôme soient présents et de même signe, et si cette
condition est vérifiée que les coefficients de la première colonne du tableau
de Routh soient de même signe (le nombre de changements de signe de la 1ère
colonne donne le nombre de pôles instables).
- ordre 1 :

- ordre 2 :
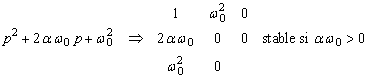
- ordre 3 :
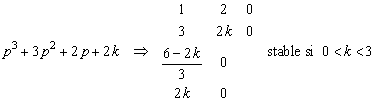
- Conclusion : Ce critère
est facile à appliquer mais il ne nous donne que les limites de réglage pour
obtenir la stabilité absolue de la boucle.

