La précision (en régime permanent) dépend, contrairement à
la stabilité, de la nature des signaux de consigne ou de perturbation. Pour
donner des résultats, nous utilisons la structure de boucle suivante :

- Erreur due à une modification de consigne
Sans perturbation, la fonction de
transfert erreur-consigne s’écrit :
Nous pouvons, pour ce système
considéré comme stable, appliquer le théorème de la valeur finale :

.
En mettant la fonction de
transfert sous la forme qui fait apparaître pôles et zéros :
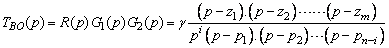
avec
i le nombre de pôles
à l’origine (intégrateurs) et
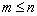
pour assurer
la causalité. Nous posons

avec
K
gain de boucle.
- Consigne échelon unité ou erreur de position :

- Consigne rampe de vitesse unité ou erreur de vitesse :
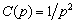
- Consigne rampe en accélération ou erreur d’accélération :

Remarque : Nous ne devons pas
oublier deux choses fondamentales. L’erreur quand elle est finie, est le plus
souvent inversement proportionnelle au gain de boucle et quand elle est nulle
(sans non-linéarité), chaque intégrateur apporte un déphasage de 90° . Un
nombre d’intégrateurs important et un gain fort sont deux conditions qui
dégradent la stabilité de la boucle.
- Erreur due à une perturbation
Avec une consigne nulle, la
fonction de transfert erreur-perturbation est :
En suivant la même décomposition
que précédemment, nous devons distinguer le nombre de pôles à l’origine
contenus dans

(

pôles) et
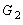
(

pôles) mais
aussi la répartition du gain respectivement
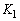
et
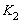
:
- Perturbation échelon unité
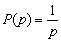
En conclusion la localisation
des intégrateurs est bénéfique si ces derniers sont situés en amont de la
perturbation. De même, si l’erreur est constante, cette dernière est plus
petite si nous augmentons le gain en amont de la perturbation.
Conclusion finale : L’automaticien doit résoudre le
dilemme stabilité-précision. Un seul paramètre de réglage en l’occurrence le
gain k est en général insuffisant, le chapitre suivant débouche
sur la synthèse d’une boucle.

