En utilisant l’outil informatique, il est
facile de représenter le lieu des pôles d’un système ou des racines de son
équation caractéristique, soit en le programmant (Mathcad), soit en utilisant
la macro-commande disponible dans le progiciel (Scilab ou Matlab).
- Exemple d’un système du 3ème ordre :
Fonction de transfert de boucle
ouverte :
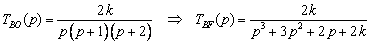
Les pôles sont les racines du
polynôme caractéristique
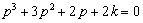
, quand le gain
k varie de 0 à l’infini, les trois racines décrivent chacune trois
branches comme visualisées sur la figure suivante. Nous indiquons quelques
valeurs caractéristiques de
k et le vecteur des pôles correspondant noté
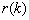
.
- Trois racines réelles stables :
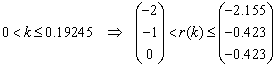
- Une racine réelle stable et deux racines complexes conjuguées
stable :
La limite de stabilité absolue est donc
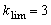
.
Pour avoir une image de la
stabilité relative, le coefficient d’amortissement des oscillations amorties
est

soit
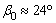
,
la valeur de gain correspondante notée

vaut
0.67.
Lieu
des pôles et concept stabilité absolue et relative
Comparaison
des réponses indicielles unitaires de la boucle pour
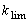
et


