Discrétisation d'une série continue
On a vu précédemment qu'une série statistique recueillie à partir de l'étude d'un caractère est dite continue quand les modalités de ce caractère peuvent prendre A PRIORI n'importe quelle valeur réelle dans tout un intervalle
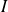de
.
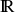A POSTERIORI, c'est-à-dire à l'issue du recueil de données, on obtient une liste de valeurs (en nombre fini en pratique) qui, à première vue, ne se différencie pas de ce qu'on peut récolter dans le cas d'une série discrète. Cependant, comme il y a une "infinité" de valeurs possibles pour les modalités d'une série continue, l'effectif de chaque modalité est le plus souvent égal à 1. Par conséquent, il n'est pas réaliste et pertinent d'essayer de synthétiser les données comme on l'a fait avec les variables discrètes : on obtiendrait des tableaux de trop grandes dimensions pour être véritablement exploitables.
Plutôt que de s'intéresser séparément à chacune des modalités d'une série continue, on fait donc le choix de regrouper celles qui sont très "voisines" en créant ce qu'on va appeler dans la suite des classes.
Exemple :
Au cours d'une séance de TP visant à mesurer expérimentalement la constante d'accélération de la pesanteur
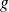, 20 étudiants ont chacun obtenu une mesure. La liste de valeurs ainsi récoltées forme une série statistique continue
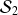, car les mesures effectuées pouvaient a priori conduire à n'importe quel nombre réel "autour" de
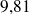m.s-2 (valeur arrondie au centième souvent retenue pour faire des applications numériques). En réalité, étant données les incertitudes liées aux appareils de mesure, les résultats obtenus sont tous des estimations arrondies au millième de la valeur de
.
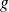La série statistique continue
est la suivante :
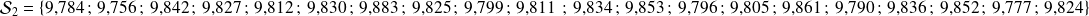
On pourrait considérer cette série comme une série discrète, mais chaque modalité aurait 1 pour effectif, et l'organisation des données sous forme de tableau ou de graphique ne permettrait pas de dégager une distribution lisible et exploitable.
