Densité de fréquence
On a vu que lors du regroupement des valeurs d'une série statistique continue, il n'était pas imposé d'utiliser des classes de même amplitude (ou étendue). Par conséquent, on ne peut pas se contenter de regarder les effectifs ou les fréquences de deux classes pour comparer leurs importances relatives : il faut rapporter ces effectifs ou fréquences aux amplitudes des classes respectives.
Définition :
C'est pourquoi, pour pouvoir comparer deux classes d'amplitudes différentes, on introduit le rapport entre la fréquence de la classe et son étendue. C'est la densité de fréquence ;
pour la classe
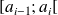de fréquence associée
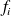, elle vaut :
.
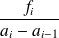Exemple :
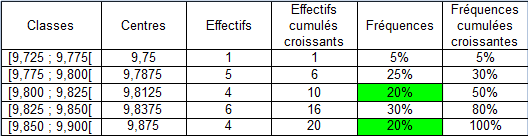
On remarque, grâce au tableau de synthèse de la série continue
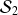des mesures de l'accélération de la pesanteur, que les classes
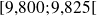et
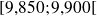ont même fréquence (à savoir
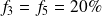). Cependant, il y a une plus forte densité de données recueillies dans la première de ces deux classes puisque son étendue est deux fois plus petite que celle de la deuxième classe.
Autrement dit, la densité de fréquence de la classe
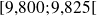est plus grande que celle de la classe
:
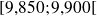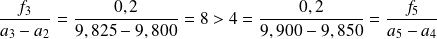
On complète en général le tableau synthétique d'une série classée par la donnée des densités de fréquence de chaque classe :
