Hypothèse de discrétisation
Le remplacement d'une série continue par une série classée utilisant les centres des classes n'est justifiée que si les valeurs observées du caractère étudié sont réparties uniformément dans chaque classe. En effet, pour que l'approximation faite en assimilant chaque valeur
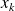d'une classe
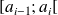à la valeur du centre
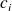ne soit pas trop grossière, il faut que l'ensemble des différences
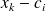se compensent à peu près (certaines étant positives et les autres négatives).
Exemple :
Dans la classe
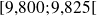de centre
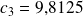de la série
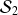(des mesures de l'accélération de la pesanteur
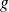rencontrée dans les exemples précédents), on retrouve les valeurs :
,
,
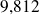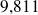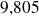et
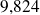. La somme des écarts entre ces valeurs et le centre
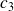est :
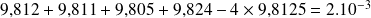m.s-2
Ainsi, la somme de ces 4 écarts est plus de 10 fois inférieure à l'étendue de la classe, égale à
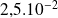m.s-2. On peut donc considérer que les 4 valeurs sont uniformément réparties dans la classe
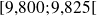, c'est-à-dire qu'on peut faire comme si les 4 valeurs étaient égales à
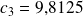m.s-2 sans que l'erreur commise soit très importante.
