Classes d'une série continue
Dans le cas d'une série continue, le statisticien doit, après avoir recueilli ses données, regrouper celles qu'il juge très voisines sous une même étiquette : le regroupement dépendra du caractère étudié, de la répartition des résultats récoltés, de l'expérience du statisticien...
Mathématiquement, ce regroupement consiste en la création de classes.
Définition : Classe d'une série continue
Les classes d'une série statistique continue sont un ensemble d'intervalles de la forme
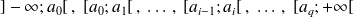tels que toutes les modalités du caractère étudié appartiennent à l'intervalle
.
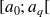Attention :
On insiste bien sur le fait que la définition donnée pour les classes d'une série continue n'impose pas aux différents intervalles d'être de même amplitude.
Exemple :
Avec la série
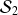(vue précédemment) des résultats de mesure de la constante
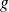, on peut, par exemple, regrouper les modalités selon les classes suivantes :
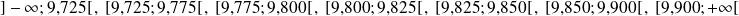
On voit que ces classes n'ont pas toutes la même amplitude : de cette façon, il n'y a pas de classe vide (c'est-à-dire de classe ne contenant aucune modalité du caractère étudié), peu de classes de très faible effectif (on le vérifiera dans l'exemple suivant) et le nombre de classes n'est pas trop petit par rapport à l'effectif total de la population.
Ce choix de classes n'est pas basé sur une analyse approfondie de la série statistique
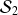. Il existe cependant certains critères empiriques permettant, par exemple, de choisir le nombre de classes avec lesquelles travailler en fonction de l'effectif de la population...
