Polygone des fréquences cumulées
On a vu précédemment que, pour justifier le remplacement d'une série statistique continue par une série classée, il faut que les valeurs recueillies du caractère étudié soient uniformément réparties dans les différentes classes. Sous cette hypothèse, on peut considérer par exemple que
des valeurs de la classe
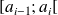sont situées dans le premier quart de l'intervalle, c'est-à-dire entre
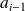et
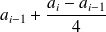: la fréquence cumulée croissante augmente de façon linéaire entre deux limites de classes
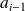et
.
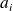Définition : Fonction fréquence cumulée
On appelle fonction fréquence cumulée ou fonction répartition de fréquences, notée
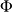, la fonction définie sur
qui, pour une valeur
réelle, donne une approximation du pourcentage d'individus pour lesquels la valeur du caractère est strictement inférieure à
. D'après ce qui précède, la fonction
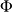est affine par morceaux ; de plus elle est continue et croissante sur
.
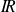Définition :
La courbe représentative de la fonction
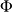est appelée polygone des fréquences cumulées.
Remarque : Fréquence cumulée associée à une valeur quelconque d'une série classée
On insiste sur le fait que la fonction
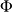ne donne, le plus souvent, qu'une approximation de la fréquence cumulée associée à une valeur
:
La fréquence cumulée fournie est exacte quand
coïncide avec une borne
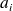d'une des classes.Pour une valeur
comprise strictement entre les 2 bornes
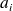et
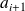d'une classe
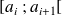, l'approximation
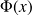de la fréquence cumulée associée à
s'obtient par interpolation linéaire à partir des points de construction du polygone des fréquences cumulées de coordonnées
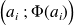et
.
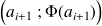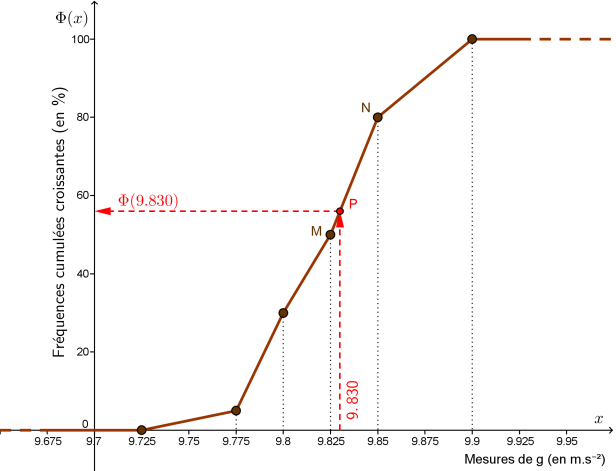
Exemple : Construction d'un polygone des fréquences cumulées croissantes
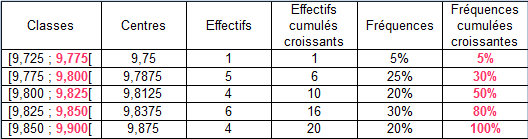
Le polygone des fréquences cumulées croissantes de la série
(des mesures d'accélération de la pesanteur) se construit à partir des points ayant pour coordonnées les bornes supérieures des classes (en abscisses) et les fréquences cumulées croissantes associées (en ordonnées). On ajoute à ces points celui d'ordonnée nulle et d'abscisse égal à la borne inférieure de la première classe. Les différents points sont alors reliés par des segments de droite, et on prolonge la courbe obtenue par des demi-droites horizontales ayant pour extrémités le premier et le dernier point du polygone (l'utilisation de tirets permet de symboliser ces demi-droites qui se prolongent vers
ou +
).
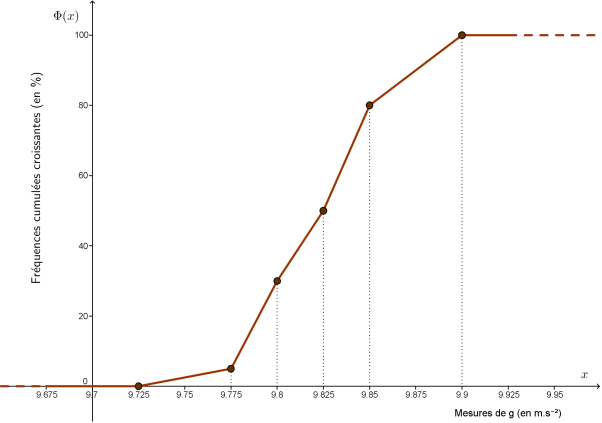
Exemple : Obtention d'une fréquence cumulée croissante par lecture graphique et par interpolation
On reprend l'exemple de la série
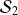(des mesures d'accélération de la pesanteur).
Sur le polygone des fréquences cumulées, on peut déterminer graphiquement
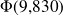, c'est-à-dire le pourcentage de mesures de
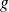inférieures à
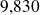m.s-2 :
On peut aussi obtenir
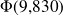par un calcul analytique :
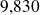est dans la classe
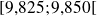, donc
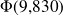est compris entre
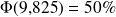et
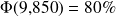. De plus, les coefficients directeurs des droites
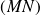et
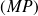étant égaux, on peut écrire :
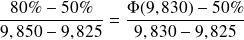
On en déduit que :
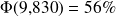, c'est-à-dire qu'environ 56% des mesures effectuées sont strictement inférieures à
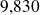m.s-2.
