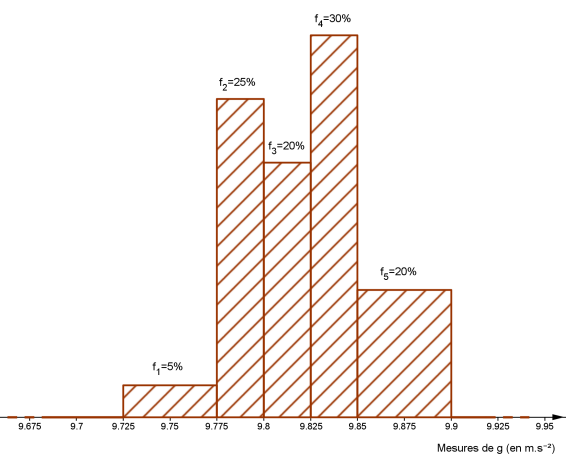Histogramme des fréquences
Comme dans le cas des séries discrètes, on peut représenter graphiquement la répartition des différentes modalités. Par contre, on n'utilise pas un diagramme en bâtons pour mettre en évidence l'importance relative des différentes modalités, car on aurait en général des diagrammes peu lisibles, constitués d'un grand nombre de bâtons de hauteurs égales.
Au lieu de cela, comme avec les tableaux synthétiques, on remplace la série continue par une série classée ; une classe
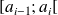est alors représentée, non pas par un bâton, mais par un rectangle de base comprise entre les abscisses
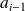et
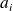. Les rectangles doivent rendre compte visuellement des fréquences des classes : ce n'est pas la hauteur des rectangles qui traduira la valeur de ces fréquences, puisque deux classes de même fréquence n'ont pas forcément la même amplitude. Pour tenir compte de l'étendue de la classe, c'est donc la surface du rectangle qui doit être proportionnelle à la fréquence de la classe : par conséquent, la hauteur du rectangle est, quant à elle, proportionnelle à la densité de fréquence de la classe.
Définition :
Le graphique ainsi obtenu est l'histogramme des fréquences de la série continue considérée : c'est donc le graphique formé de rectangles ayant comme largeur sur l'axe des
, l'étendue de la classe, et des aires proportionnelles aux fréquences des classes. En toute rigueur, un histogramme ne comporte pas d'axe des ordonnées.
Attention :
On insiste encore une fois sur le fait que les hauteurs des rectangles dans l'histogramme des fréquences sont proportionnelles aux densités de fréquence et non pas aux fréquences.
Exemple :
On a vu dans l'exemple précédent que les classes
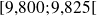et
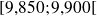de la série
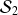(des mesures d'accélération de la pesanteur) avaient même fréquence (
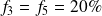) mais des amplitudes différentes. Graphiquement, on traduit ces deux renseignements par des rectangles de même surface (correspondant à la fréquence commune) mais de bases inégales (proportionnelles aux étendues des deux classes) : les hauteurs des deux rectangles s'obtiennent donc en faisant le rapport entre la surface (la fréquence de la classe) et la base (l'étendue de la classe). Autrement dit, les hauteurs sont proportionnelles aux densités de fréquence des classes.
En agissant ainsi pour chaque classe, on obtient finalement l'histogramme des fréquences suivant pour la série classée issue de la série
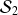des exemples précédents :
