En repartant de la forme générale d'un système bouclé, il est pratique de se donner une forme d'écriture homogène, qui permet de séparer le fonctionnement idéal, ce que l'on cherche à obtenir, des effets correctifs liés aux limitations en gain, en bande passante, du système réel.

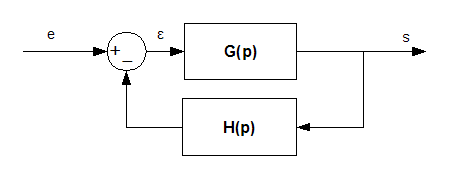
Le schéma bloc général d'un système bouclé est représenté ci-dessous. Dans ce schéma, G(p) représente la fonction de transfert de la chaîne directe, H(p) la fonction de transfert de la chaîne de retour, celle qui assure le contrôle du système.

En général G(p) comporte un gain en puissance, dont les paramètres sont souvent mal définis, alors que H(p) est un système de mesure, éventuellement passif, qui peut être réalisé avec une bonne précision. L'exemple typique de cette situation est un schéma d'amplificateur construit avec amplificateur opérationnel : G(p) représente le gain en boucle ouverte de l'amplificateur opérationnel, H(p) est un diviseur passif construit avec des composants qui peuvent être de précision.

2.3.a Le cas idéal : un gain infini

En utilisant les transformations de schémas blocs énoncées au paragraphe 2.2, le schéma bloc général peut être représenté sous une nouvelle forme :

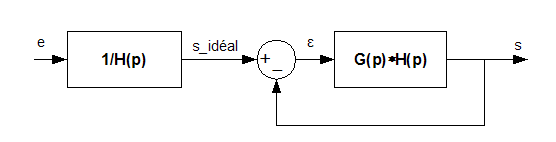
Le premier bloc ( 1/H(p) ) représente l'inverse de la fonction de transfert de la chaîne de retour. La boucle à retour unitaire construite autour de la fonction de transfert T_bo(p) = G(p)*H(p) concentre tous les « défauts » du système.

Cette fonction de transfert (T = G*H) est ce que l'on appelle couramment le gain de boucle. Il est important de noter que ce gain de boucle contient à la fois les caractéristiques de la chaîne directe et celles de la chaîne de retour.

Si le gain de boucle a un module toujours très grand, on peut approcher la fonction de transfert en boucle fermée par son expression dans le cas idéal (G*H infini) :

T_idéal(p) = 1/H(p)

2.3.b Les caractéristiques réelles : un système bouclé à retour unitaire

Une manipulation simple permet d'écrire la fonction de transfert en boucle fermée sous la forme :

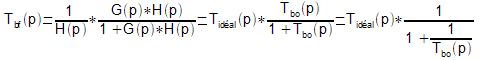
Une autre forme, souvent pratique, est d'introduire le gain de boucle sous la forme d'une fraction :

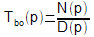
Il vient alors :

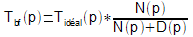
Ou encore, si, ce qui est un cas fréquent, N(p) est un gain statique constant T₀ :

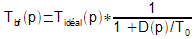
Ces deux dernières expressions nous permettront de calculer, sans grand effort, les caractéristiques en boucle fermée de nombreux systèmes simples. Il est à noter que si le numérateur de la fonction de transfert est une constante (T₀), l'ordre du système n'est pas modifié par la boucle.