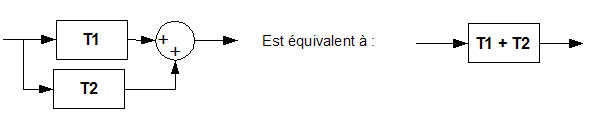Résoudre
un
système d'équations linéaires revient le plus
classiquement à faire des substitutions pour remplacer une
variable, dans une équation, par des combinaisons d'autres
variables. Ce type de calcul nécessite une certaine intuition
pour arriver rapidement au bout, les schémas blocs permettent
de visualiser graphiquement la structure d'un système, et
servent de guide dans les manipulations. Nous nous contenterons ici
d'indiquer quelques opérations élémentaires dont
nous aurons souvent besoin lors de l'étude des systèmes
bouclés. Les démonstrations sont triviales, il suffit
d'effectuer directement le calcul algébrique équivalent
pour se convaincre de l'exactitude des résultats annoncés
2.2.a Déplacer
un soustracteur
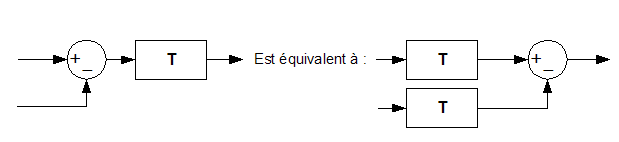
Réciproquement :
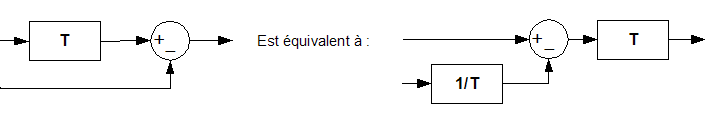
2.2.b Déplacer
un point de prélèvement

Réciproquement :
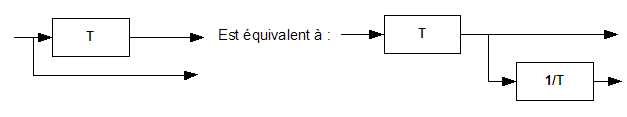
2.2.c Le
système bouclé générique
Enfin,
deux
équivalences dont nous nous servirons constamment :
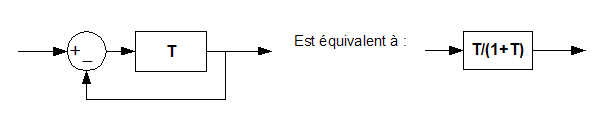
Cette
« réduction de boucle » est à la
base de toutes les études, de stabilité des
systèmes
notamment.
L'équivalence
qui précède, qui exprime la notion de retour de la
sortie d'un système vers son entrée, ne doit pas
être
confondue avec la construction d'une fonction de transfert comme
somme de deux fonctions de transfert :