Reprenons encore une fois l'exemple 3. On souhaite calculer la probabilité d'être déclaré positif sans savoir si on est malade ou non.

En effet, un système complet d'évènements est constitué par les deux évènements {"être malade " ; "ne pas être malade"}. Ils sont donc disjoints , d'où le résultat ci-dessus.

Or, nous savons calculer les deux termes de la somme en utilisant l'arbre résumant la situation.

Il suffit donc de calculer la probabilité de toutes les branches qui ont pour "terminus" P_o.

Cela donne P(P_o) = 1/3 x 8/10 + 2/3 x 1/10 = 10/30 = 1/3.

On notera que pour atteindre P_o on peut circuler sur une branche qui conduit à P_o ou bien sur l'autre branche qui conduit à P_o.

Enfin, notons que la première partie (colonne de gauche) de l'arbre résumant la situation doit toujours représenter un système complet d'évènements.  

Soit (Ω ; P) un espace probabilisé. Soit  A_i i appartenant à {1; 2 ; ...; n} un système complet d'évènements. Soit B un évènement de Ω. On a alors :

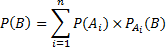
 La situation peut être illustrée par le schéma suivant :

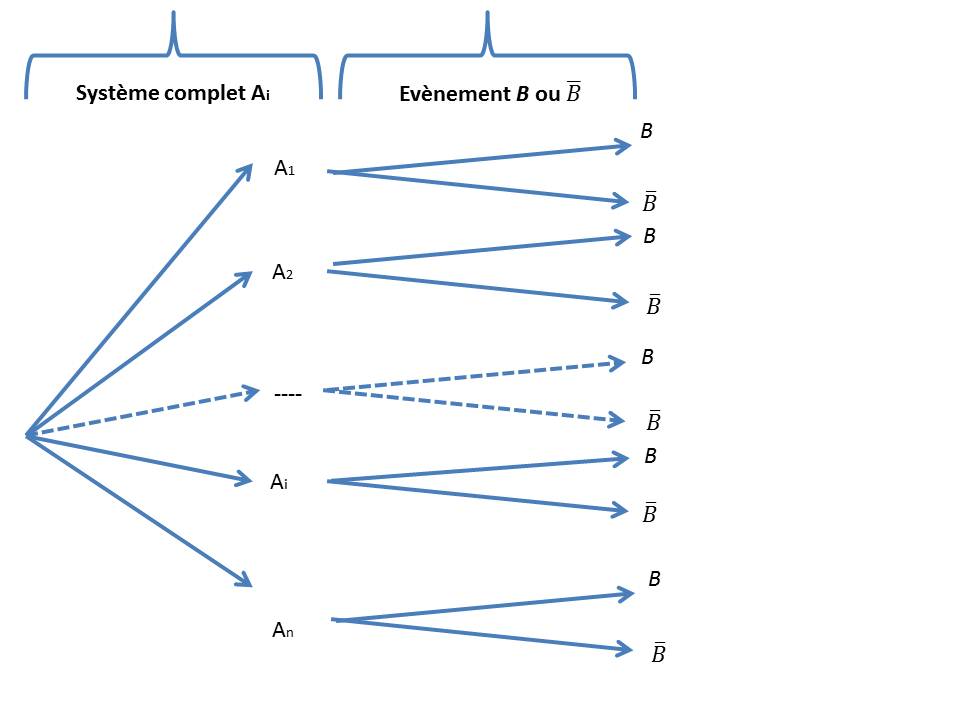
On veut connaitre la probabilité de tous les chemins qui arrivent à B. Pour cela on passe par A₁ ou bien par A₂ ou bien par ... ou bien par A_i ou bien par ... ou bien par A_n. 

On doit donc effectuer la somme des probabilités de chaque branche.

Pour calculer la probabilité de chaque branche, on utilise la formule des probabilités composées (vue et illustrée plus haut dans le cours).

Par exemple :

D'où la formule...