Principe de résolution des structures hyperstatiques

Pour simplifier l'étude de la déformée, nous allons décomposer le chargement de la structure en une succession de chargements distincts :

- le premier chargement sur la SIA est composé du chargement de la structure hyperstatique (sans les inconnues hyperstatiques libérées). Nous nommerons cette structure la SIA₀^[1] ;

- le second chargement, nommé SIA₁^[2], contient uniquement la première inconnue hyperstatique ;

- le troisième chargement, nommé SIA₂^[3], contient uniquement la seconde inconnue hyperstatique ;

- ...

- le H + 1 chargement, nommé SIA_H^[4], contient uniquement la H^ème inconnue hyperstatique ;

Pour notre exemple, nous avons donc les structures suivantes :

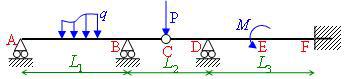
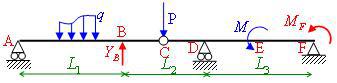
En superposant ces 3 SIA, nous obtenons notre SIA du départ, équivalente à la structure hyperstatique dans le cas où :

- f_B = 0 ;

- ω_F = 0.

Nous trouverons les inconnues Y_B et M_F en écrivant les deux équations suivantes :

⇒ f_B = 0 = f_B0 + f_B1 + f_B2 avec f_B0 : flèche en B de la SIA₀, f_B1 : flèche en B de la SIA₁ et f_B2 : flèche en B de la SIA₂.

⇒ ω_F = 0 = ω_F0 + ω_F1 + ω_F2

‣ f_B1 est proportionnel à Y_B ;

‣ f_B2 est proportionnel à M_F ;

‣ f_B est donc fonction de Y_B et de M_F ;

‣ ω_F1 est proportionnel à Y_B ;

‣ ω_F2 est proportionnel à M_F ;

‣ ω_F est donc fonction de Y_B et de M_F ;

On obtient ainsi un système de 2 équations avec nos 2 inconnues.