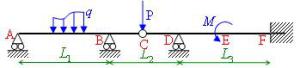
Analyse d'une structure quelconque
Soit la structure quelconque suivante : |  Schéma statique de la structure quelconque |
Cette structure est hyperstatique de degré 2 (pour la décomposition minimale, nous avons 6 équations et 8 inconnues). Nous la noterons « SH[1] ».
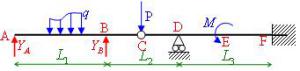
a) SIA :
Nous allons donc libérer 2 inconnues, appelées inconnues hyperstatiques.
La structure ainsi obtenue deviendra isostatique dans le cas où les inconnues libérées sont considérées comme un chargement. Nous la noterons « SIA[2] » (comme structure isostatique associée).
Nous pouvons ainsi obtenir, par exemple, les SIA suivantes :
Attention : il ne faut surtout pas prendre la structure suivante : |  SIA incorrecte |
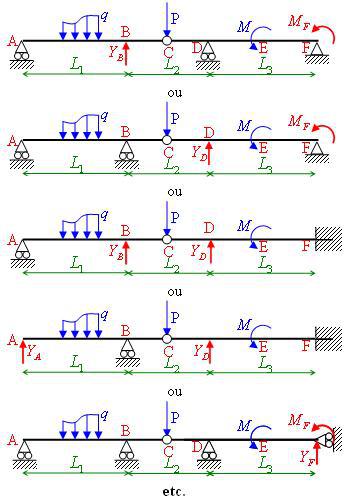
En effet, si l'on retire les inconnues libérées (YA et YB), nous nous retrouvons avec un mécanisme (la barre AC s'effondre).
Autre possibilité : dans ces différents exemples, nous avons choisi de libérer des inconnues au niveau des appuis. Nous pouvons aussi libérer des inconnues internes :
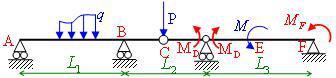
Si on pose le moment MD dans un sens à gauche de l'articulation, il est impératif de le replacer dans l'autre sens à droite.
Dans le cas où l'on réussi à déterminer les inconnues ainsi libérées sans utiliser le PFS, le problème est résolu.
