Conditions d'équivalence
Comparons l'une des SIA à la structure de départ (SH) :

Si les structures sont identiques, elles doivent avoir le même comportement, et donc la même déformée !
Comparons maintenant les deux déformées :

Les déformées seront identiques :
- si la force YB annule la translation en B ;
- et si le moment MF annule la rotation en F.
Notre structure étant hyperstatique de degré 2, il nous manque 2 équations (appelées conditions d'équivalence) pour la résoudre. Ces deux équations sont basées sur la déformée. Nous venons de les trouver :
- fB = 0 ;
- ωF = 0.
Comme nous savons déterminer l'équation de la déformée d'une telle structure, nous pouvons résoudre les inconnues hyperstatiques.
Pour déterminer rapidement les conditions d'équivalence, 3 techniques sont possibles :
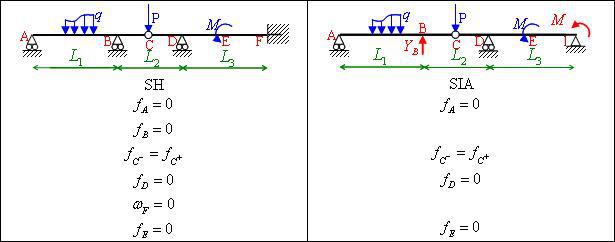
écrire les conditions limites de la déformée de la structure hyperstatique et de la structure isostatique associée :
Les conditions d'équivalence correspondent aux conditions limites que l'on trouve sur la structure hyperstatique mais que l'on ne retrouve pas sur la structure isostatique associée :
réfléchir aux mouvements libérés lors du passage de la SH à la SIA :
- en supprimant l'appui simple en F, nous y avons libéré la translation verticale → fB = 0 ;
- en changeant l'encastrement en F par une articulation, nous y avons libéré la rotation → ωF = 0.
regarder tout simplement les inconnues libérées :
- pour les forces, les translations y sont nulles ;
- pour les moments, les rotations y sont nulles ;
YB : force verticale en B → fB = 0 ;
MF : moment en F → ωF = 0.
⇨Remarque : pour les relâchements internes, les rotations relatives y sont nulles.





