Écart-type
La variance d'une série statistique que l'on vient de définir est un paramètre de dispersion qui joue le même rôle que l'écart absolu moyen par rapport à la moyenne, mais qui a, en plus, l'avantage d'être plus aisé à manipuler dans les calculs du fait du remplacement des valeurs absolues présentes dans la définition de l'écart moyen par des carrés. Cependant, ce remplacement a une conséquence regrettable en terme de dimension physique : en effet, si les valeurs d'une série statistique sont des grandeurs physiques dimensionnelles, alors la variance de cette série n'a pas la même dimension que les valeurs en question.
Définition :
Pour se donner un paramètre de dispersion conservant les qualités de la variance et étant de même dimension que les valeurs de la série à laquelle il se réfère, on introduit l'écart-type: l'écart-type
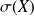d'une série statistique
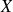est tout simplement la racine carrée de la variance de cette série.
Fondamental :
La fonction racine carrée étant croissante sur
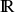, l'interprétation de l'écart-type est équivalente à celle de la variance et donc de l'écart absolu moyen : plus l'écart-type d'une série est grand, plus les valeurs de cette série sont dispersées.
Formellement, on a, toujours avec les mêmes notations que précédemment :
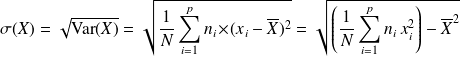
Exemple :
Pour les étudiants
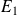et
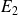des exemples précédents, on avait calculé :
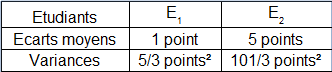
Les variances, à la différence des écarts absolus moyens, s'expriment ici en " points2 " ce qui n'a guère de signification. On préfère donc comparer la dispersion des notes des deux étudiants au moyen de la racine carrée des variances, c'est-à-dire des écarts-types. Or on a bien :
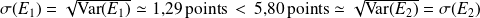
On remarque que les écarts-types restent dans les mêmes ordres de grandeur que les écarts absolus moyens : ils en fournissent en général une bonne approximation.
