Variance
L'écart absolu moyen vu précédemment présente l'avantage de tenir compte de toutes les valeurs d'une série statistique pour donner une indication sur la dispersion de ces valeurs. Par contre, il y a un inconvénient en termes de calculs à utiliser l'écart moyen : la formule qui le définit fait intervenir des valeurs absolues souvent délicates à manipuler (les calculatrices ne les prennent pas forcément en charge ; on ne peut pas faire grand chose avec la valeur absolue d'une somme...).
Par conséquent, plutôt que de travailler avec des écarts en valeurs absolues, on travaille avec les carrés des écarts : les carrés de nombres étant toujours positifs, il n'y a pas de compensation entre des écarts négatifs et des écarts positifs ; de plus, la fonction carrée étant croissante sur
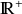, le carré d'un écart est d'autant plus grand que l'écart lui-même est grand.
Ainsi, en remplaçant les écarts en valeurs absolues
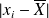par les carrés des écarts
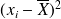dans la formule de définition de l'écart absolu moyen, on obtient à nouveau un indicateur qui prend une valeur positive d'autant plus grande que beaucoup de modalités
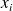sont éloignées de la valeur moyenne
.
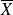Définition :
Finalement, on appelle variance d'une série statistique
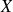, et on note Var
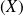, la moyenne des carrés des écarts entre les valeurs de la série et la valeur moyenne. Avec les mêmes notations que précédemment, on a :
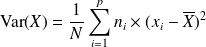
La variance est un nombre positif qui est d'autant plus élevé que les valeurs de la série sont dispersées.
Méthode : Formule de Koenig
On montre que la variance d'une série statistique
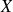peut aussi se calculer par une autre formule souvent plus facile à appliquer et appelée formule de Koenig :
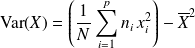
Cette formule s'interprète en disant que la variance d'une série statistique
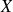est la différence entre la moyenne des carrés des valeurs de cette série et le carré de la moyenne des valeurs de cette série:
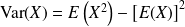
Exemple :
Reprenons encore le cas des notes des étudiants
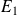et
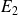des exemples précédents :
La variance de la série des notes de l'étudiant
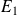est donnée par :
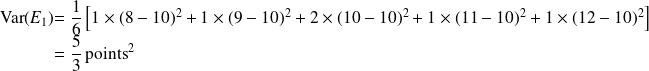
Ou, en utilisant la formule de Koenig :
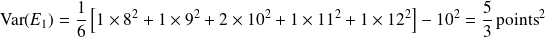
De la même façon, on calcule la variance de la série des notes de l'étudiant
:
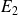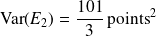
On peut finalement faire la même constatation que celle faite grâce aux écarts absolus moyens : comme la variance Var
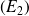est beaucoup plus grande que la variance Var
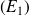, les notes de l'étudiant
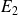sont beaucoup plus dispersées que celles de l'étudiant
.
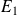