Etendue
Définition :
Un des paramètres de dispersion les plus simples est l'étendue de la série statistique. Il s'agit de la différence entre la plus grande modalité
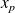de la série et la plus petite
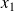: étendue=
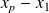
Elle donne bien un renseignement sur la répartition des valeurs de la série statistique : plus l'étendue est grande, plus l'écart entre la plus petite et la plus grande modalité de la série est importante, et donc plus les valeurs de la série peuvent être dispersées sur un grand intervalle.
Exemple :
On a relevé les notes obtenues à 6 contrôles successifs par trois étudiants
,
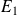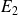et
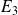d'un même groupe :
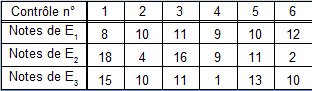
On peut vérifier que les moyennes arithmétiques de ces trois étudiants sont toutes égales à 10. Cependant cette moyenne ne reflète pas du tout les différences de comportement entre ces 3 étudiants :
En effet, il semble que l'étudiant
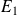fournisse un travail régulier, car toutes ses notes sont proches de 10.L'étudiant
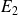, au contraire, ne travaille apparemment que par rapport à sa dernière note afin de s'assurer d'avoir 10 de moyenne sans faire plus d'effort que nécessaire.Et l'étudiant
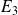a toujours des résultats convenables, sauf à un contrôle pendant lequel il ne se sentait vraisemblablement pas bien.
Le calcul de l'étendue des séries statistiques constituées des notes des étudiants
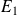et
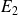permet de mettre en évidence la différence entre les comportements scolaires de ces deux étudiants :
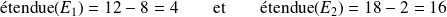
L'étendue de
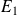est beaucoup plus faible que celle de
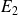, ce qui traduit bien le fait que les notes de
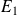sont beaucoup moins dispersées autour de la note moyenne 10 que celles de
.
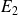L'étendue reste cependant un paramètre de dispersion très grossier, car elle ne permet pas de refléter le fait que les notes de l'étudiant
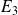sont, à une exception près, toutes voisines les unes des autres. Effectivement, l'étendue de
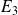est très élevée : étendue
.
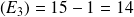On va voir que dans de telles situations, un autre paramètre de dispersion simple, l'écart inter-quartiles, permet d'affiner les informations fournies par l'étendue...
