Écart absolu moyen
Les deux paramètres de dispersion que l'on vient de voir (l'étendue et l'écart inter-quartiles) n'utilisent que deux valeurs (modalités extrêmes ou quartiles) de la série statistique étudiée pour estimer la dispersion des valeurs de la série. L'information qui en résulte n'est donc pas très précise.
Définition :
Pour tenir compte de toutes les valeurs de la série dans l'estimation de la dispersion de ces valeurs, on peut calculer la moyenne des écarts entre chaque valeur de la série et la moyenne arithmétique de cette série. C'est l'écart absolu moyen par rapport à la moyenne qu'on notera "eamm" : pour une série statistique notée
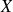d'effectif total
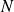, de modalités
,
, ...,
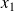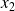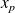et d'effectifs
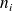, on a :
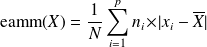
Les valeurs absolues sont nécessaires pour que les écarts positifs ne soient pas "compensés" par les écarts négatifs.
Plus l'écart absolu moyen par rapport à la moyenne est élevé, plus il y a de valeurs éloignées de la moyenne : l'écart absolu moyen est donc bien un paramètre de dispersion, c'est-à-dire un indicateur de l'étalement des valeurs recueillies.
Remarque :
On peut, de manière similaire, définir un écart moyen par rapport à la médiane quand on juge que la médiane est un paramètre de position plus approprié à l'étude d'une série statistique que la moyenne arithmétique.
Exemple :
La répartition "modalités-effectifs" de la série des notes des étudiants
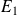et
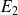des exemples précédents se synthétise par le tableau suivant :
On a vu précédemment que la moyenne de cette série statistique était :
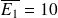. La moyenne des écarts entre chaque note et cette note moyenne est :
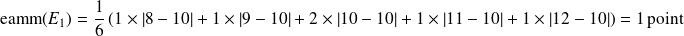
Cela signifie donc que, en moyenne, les notes de l'étudiant
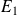sont éloignées d'1 point par rapport à sa moyenne.
Le même raisonnement concernant l'étudiant
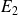conduit à l'écart moyen :
.
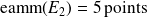L'écart moyen des notes de l'étudiant
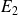par rapport à sa moyenne est beaucoup plus grand que l'écart moyen des notes de
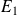: cela traduit ce que l'on avait constaté dès le début, à savoir que les résultats de l'étudiant
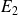sont bien plus irréguliers que ceux de l'étudiant
.
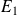