Moyenne arithmétique
La médiane, que l'on a vue précédemment, est un paramètre de position donnant une valeur autour de laquelle se répartissent les modalités de la série. On a remarqué qu'elle présentait la particularité de ne pas être sensible aux valeurs extrêmes : cela peut être intéressant quand ces valeurs extrêmes correspondent à des valeurs aberrantes (mesures de grandeurs physiques peu réalistes par exemple). Cependant, et du même coup, elle ne prend guère en compte la dispersion de l'ensemble des valeurs. De plus, la médiane n'est pas donnée par une formule algébrique et est difficilement manipulable dans le cadre d'opérations linéaires simples.
C'est pour ces raisons qu'on préfère, dans certains cas, utiliser la moyenne arithmétique des valeurs prises par la série statistique.
Définition :
Notant
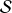une série statistique discrète d'effectif
;
,
, ...,
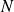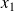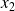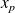ses modalités ;
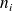et
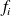les effectifs et fréquences associés à ces modalités ; la moyenne arithmétique de
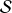, notée
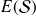ou
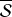, est le nombre défini par :
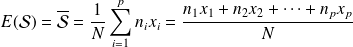
Ou encore, puisque
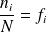, par :
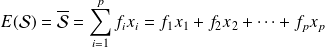
Exemple : Application de la formule de calcul de la moyenne arithmétique
On a vu dans les exemples précédents que c'était la pointure 39 qui était médiane dans la série des pointures des ventes mensuelles du magasin de chaussure :
La pointure moyenne, quant à elle, est donnée par :
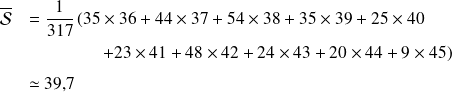
Exemple : Sensibilité de la moyenne aux valeurs extrêmes
On gardera bien en mémoire que la moyenne arithmétique est, à la différence de la médiane, sensible aux valeurs extrêmes ou aberrantes.
Si, par exemple, dans une entreprise, 9 salariés sont payés
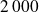Euros mensuels, tandis que le directeur peut compter sur un revenu mensuel de
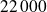Euros, alors le calcul de la moyenne arithmétique de la série
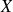des salaires des employés de l'entreprise conduit à une valeur non représentative :
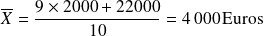
La moyenne est effectivement supérieure au salaire de la quasi-totalité des employés de l'entreprise !
Pour atténuer les effets des valeurs extrêmes, on peut calculer la moyenne d'une série après l'avoir tronquée d'un certain pourcentage des valeurs les plus faibles et des valeurs les plus fortes.
