Médiane
Définition :
Pour permettre de situer autour de quelle valeur les modalités d'une série statistique se répartissent, on peut donner la médiane de cette série statistique : il s'agit d'une valeur
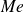qui sépare la famille des données recueillies et rangées dans l'ordre croissant (en répétant les données identiques autant de fois qu'elles ont été obtenues) en deux sous-familles de même effectif.
Attention :
Pour une même série, il peut exister plusieurs valeurs possibles pour la médiane, et une médiane n'est pas forcément une modalité de la série.
Plus précisément, on distingue deux cas suivant la parité de l'effectif total
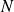de la population :
Si
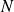est impair, avec
(
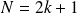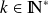), en notant
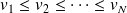(avec
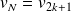) les données recueillies de la série statistique, alors on a :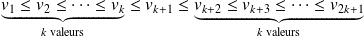
La valeur
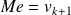sépare la série statistique ordonnée en deux sous-séries de même effectif : il s'agit donc de la (seule) médiane (possible).
Si
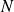est pair, avec
(
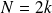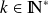), en notant
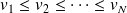(avec
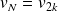) les données recueillies de la série statistique, alors on a :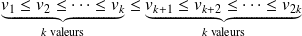
Toute valeur
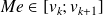sépare la série statistique ordonnée en deux sous-séries de même effectif : une telle valeur est donc une des médianes de la série. (Si
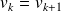, il n'y a en réalité qu'une seule valeur possible).
Remarque :
La médiane n'est pas sensible aux valeurs extrêmes : si, par exemple, on échange la plus grande valeur d'une série statistique par une valeur beaucoup plus grande, la médiane reste inchangée.
Exemple :
Reprenons la série statistique discrète des ventes mensuelles d'un magasin de chaussure :
L'effectif total de cette série est impair :
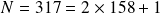. En ordonnant les valeurs de cette série statistique, on obtient :
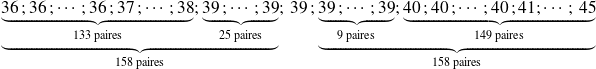
Cette série n'a donc qu'une valeur médiane : la pointure
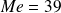qui sépare la série statistique en deux sous-séries d'effectifs égaux à 158. Ce renseignement permet de savoir que les pointures des paires de chaussures vendues se répartissent équitablement autour de la pointure 39.
Imaginons maintenant que le magasin de chaussure propose à un client fidèle, basketteur professionnel, des modèles de chaussure à sa pointure, à savoir du 52. Si ce client fidèle achète 8 paires de chaussures dans le mois, l'effectif de la série statistique passe à 325, mais la médiane reste inchangée, car c'est encore une pointure 39 qui va séparer la série en deux sous-séries d'effectif 162. On dit que la médiane n'est pas influencée par les valeurs extrêmes.
