Quartiles
Définition :
Par extension de la notion de médiane, on appelle, pour une série aux valeurs ordonnées dans l'ordre croissant, quartiles les nombres
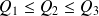qui divisent l'ensemble des valeurs de la série en quatre parties égales.
Attention :
Comme la médiane, les quartiles ne sont pas forcément uniques et ne sont pas toujours des modalités de la série. Leur détermination dépend également de la parité de l'effectif total et de la parité de l'effectif des sous-séries séparées par la médiane.
Remarque :
Le deuxième quartile
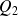n'est autre que la médiane
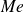de la série.
Exemple :
On a vu dans l'exemple des ventes mensuelles des paires de chaussures d'un magasin (comptées selon la pointure) que la médiane
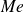, c'est-à-dire le deuxième quartile
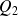, de la série était la pointure 39, et qu'elle séparait la série en deux sous-séries d'effectif 158. Les deux sous-séries ont maintenant un effectif pair, donc le premier quartile
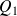doit être un nombre qui sépare la première sous-série (ordonnée) en deux familles d'effectif 79 ; de même le troisième quartile
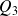doit être un nombre qui sépare la deuxième sous-série en deux familles d'effectif 79. On peut présenter la recherche de ces quartiles dans le tableau suivant :
D'après le tableau précédent, on voit qu'on peut choisir n'importe quel nombre dans l'intervalle
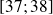comme premier quartile
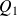. Il est souvent d'usage de choisir le centre de l'intervalle dans une telle situation.
Le troisième quartile
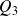est unique, par contre, et correspond à la pointure 42.
