Cherchons la réponse s(t) à un échelon unité : pour t < 0 e(t) = 0 et pour t > 0 e(t) = 1. On suppose que s(t) est une variable d'état et que s(0) = 0 et ds(0)/dt = 0.

L'équation du système est : 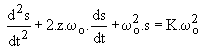. Pour trouver la solution générale de l'équation sans second membre, nous devons résoudre l'équation caractéristique :

. On aura donc trois cas suivant le signe du déterminant.

A) Cas d'un fort amortissement : z > 1

Dans ce cas, l'équation caractéristique a deux racines réelles négatives x₁ et x₂ avec :

.

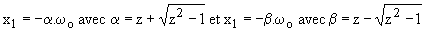Notons que si le système est très amorti soit z >> 1 les deux racines sont d'ordres de grandeur très différents : a >> 1 et b << 1. Si le système est peu amorti soit z » 1 alors a et b sont du même ordre de grandeur.

La solution générale de l'équation sans second membre est :

La solution particulière est s₂ = K. D'où la solution :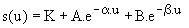

Cherchons la valeur des constantes d'intégration :

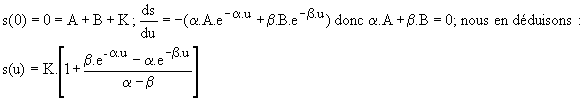
La fig.2 donne la réponse s(u)/K pour plusieurs valeurs de l'amortissement.

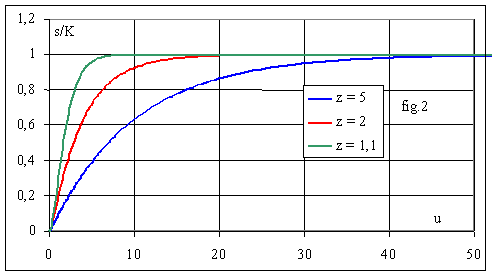
On constate :

que le régime permanent est quasi atteint au bout d'un temps d'autant plus grand que l'amortissement est grand.

pour les forts amortissements les deux constantes de temps sont t₁=1/a.w_o et t₂=1/b.w_o avec t₁<< t₂. La réponse est peu différente de celle d'un premier ordre de constante de temps t₂. La différence principale se situe à l'origine : le graphe du deuxième ordre a une tangente de pente 0 au lieu d'avoir une pente 1/ t.

B) Amortissement critique : z = 1

Si z = 1, l'équation caractéristique a une racine double -w_o. La solution est alors de la forme :

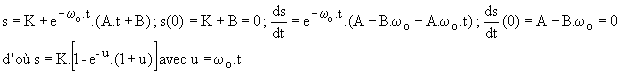
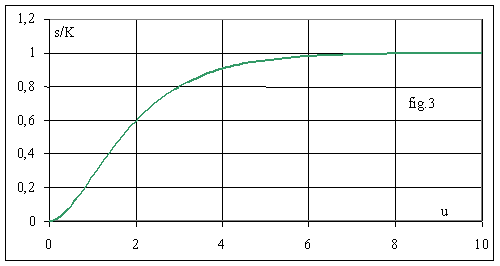
La fig.3 donne la réponse . On constate un graphe du type de ceux obtenus pour z >1.

C) Amortissement faible : z < 1

Pour z < 1, l'équation caractéristique a deux racines complexes conjuguées :

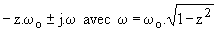; la solution générale est de la forme :

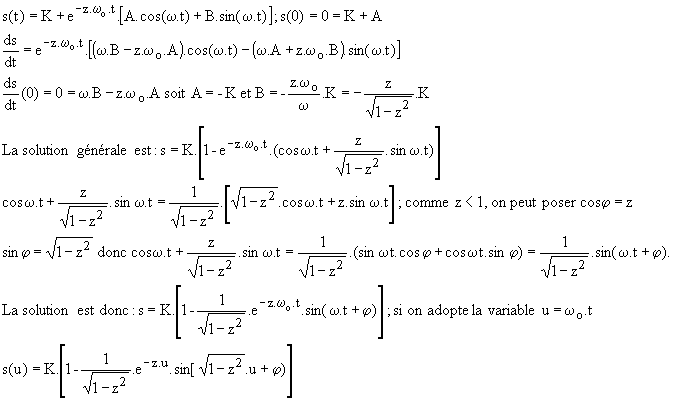
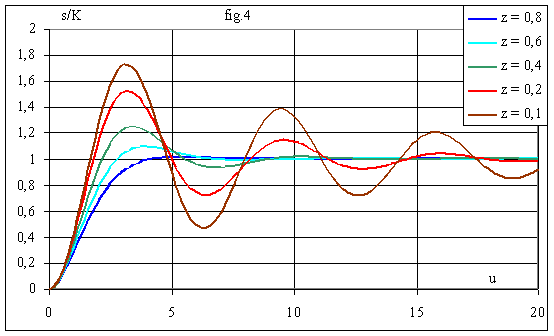
La fig.4 donne s(u)/K pour plusieurs valeurs de z

.

Cherchons l'amplitude des extréma : ds/dt étant proportionnelle à sin (w.t), la dérivée s'annule pour .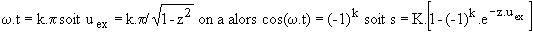

les valeurs impaires de k correspondent aux maxima et les valeurs paires au minima.

Si on appelle d le dépassement l'écart relatif en valeur absolu entre la valeur de régime permanent et l'extrêma, on a .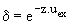

La fig.5 donne les valeurs successives des extréma en fonction de l'amortissement :

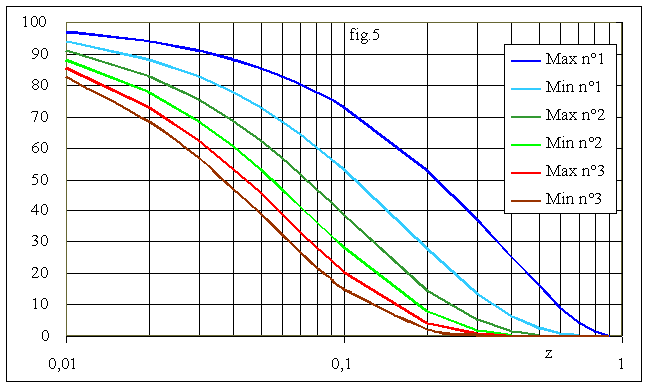
On constate que :

lorsque z tend vers 0 les oscillations sont très peu amorties

pour 0,71 < z < 1, les oscillations sont quasi imperceptibles puisque le premier dépassement n'atteint pas 5 % et le deuxième est inférieur à 1 %. Cette limite de z correspond à celle rencontrée dans l'étude en régime harmonique: il n'y a des oscillations perceptibles que lorsque la fonction de transfert présente une résonance.

D) Temps de réponse

C'est le temps t_r au bout duquel la fonction s (t) est égale à la valeur K de régime permanent à ± 5% , c'est à dire que 0,95.K < s(t) < 1,05.K. La fig.6 montre l'évolution du temps de réponse avec l'amortissement ; on a représenté u_r = w_o.t_r :

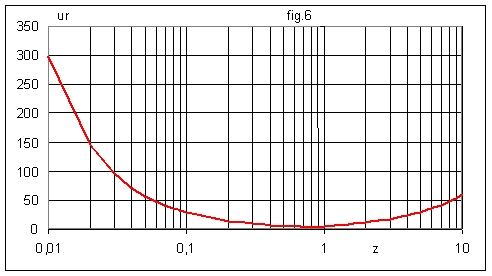
On a un temps de réponse minimal pour z = 0,71 correspondant à u_r = 2,9.

Pour z < 1, la courbe du temps de réponse devient discontinue car par paliers, on ajoute une demie période d'oscillation soit Du_r = p.