The op-amp is a differential amplifier, it amplifies the quantity (V+ - V-), indicated by ε.

Vs = A.(V+ - V-) = A.ε

A real op-amp has tipically a very large gain A on the range 10⁴ – 10⁶ which depend on the type. In the ideal model, we will often consider it as infinite .

Vs is limited to the values called Saturation Voltages, Vsat+ and Vsat-, which are close to Valim+ and Valim- (± 2V).

Vsat+  = Valim+ -1 to 2V (for ex. -13 to -14 V for Valim+ = -15V) and Vsat- = Valim- +1 – 2 V (for ex. : -13 to -14 V for Valim- = 15V).

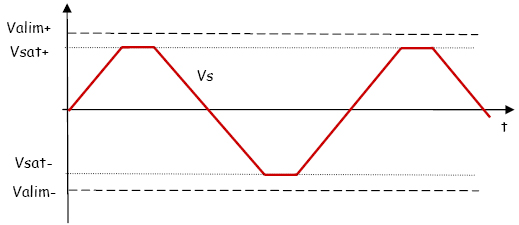
The output voltage cannot be greater than Vsat + and Vsat -

Even if the power supply of the op-amp is perfectly symmetrical, the absolute values of Vsat+ and Vsat- are close but not identical. They depend mainly from the current Is which is drawn by the output.

The real output characteristic Vs (ε) is then as follows :

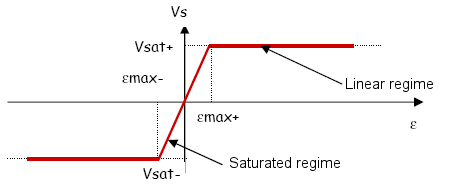
The relationship Vs (ε) is linear only for small values of ε, which are bound to εmax and εmin : beyond these values, the output is saturated.

For example, if Vsat = 14V and A = 10⁵, εmax+ = Vsat/A = 140µV

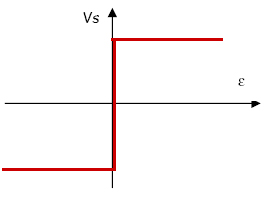
If the op-amp is not saturated, ε is then very low. In the ideal model, ε is considered zero, which is as we considered A = infinite

In this way, we obtain the characteristics of Vs (ε) of the ideal op-amp :

Moreover, the op-amp input currents I+ and I- are very weak (hundreds of nA in the case of bipolar transistor inputs - BJT, a few pA in the case of field-effect transistor inputs - FET).
In the ideal model  : I+ = I- =   0

Ideal model of the op-Amp I+ = I- =   0 A = ∞ Linear regime: ε = 0 et Vsat- < Vs < Vsat+ Nonlinear regime (or saturated) : ε ≠ 0 and Vs = Vsat+ or Vs = Vsat- This model is often used to perform calculations on the classical configurations of the op-amp.

NB : In some op-amp configurations called “rail to rail” the Saturation Voltages are equal to the power-supply voltages (within 50 mV error).