La stabilité absolue est insuffisante, une réponse oscillatoire, même amortie, peut être inacceptable dans bien des situations courantes. Par exemple, l'intégrateur avec retard précédent, dans sa version stable, présente un dépassement de 50 % dans la réponse à un échelon. Si on imagine que ce système représente la réponse de la direction assistée d'un véhicule à une rotation du volant, il est inutile de décrire la surprise du conducteur face à un tel comportement.

5.2.a Amortissement et distance au point critique

L'expression générale de la relation entre fonction de transfert en boucle ouverte et fonction de transfert en boucle fermée, exprimée en analyse harmonique, permet de préciser les choses :

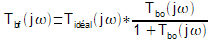
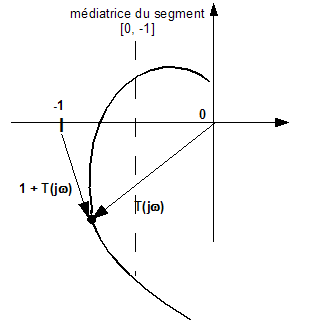
Le facteur correctif, qui prend en compte les « défauts » du système, a une interprétation géométrique simple dans le plan de Nyquist :

• Le module du numérateur (|T_bo(jω)|) représente la distance d'un point du diagramme à l'origine du plan complexe.

• Le module du dénominateur (|1 + T_bo(jω)|) représente la distance de ce même point de la courbe au point critique.

En analyse harmonique, le système en boucle fermée présente une résonance si, pour certaines valeurs de la fréquence, le diagramme de Nyquist se rapproche plus du point critique que de l'origine du plan complexe.

Plus le diagramme de Nyquist passe près du point critique, plus forte sera la résonance en boucle fermée.

Évidemment, une résonance en régime harmonique et un dépassement en réponse temporelle ne sont pas synonymes, l'exigence d'une réponse sans dépassement est généralement un peu plus sévère que celle d'absence de maximum dans la courbe du module du gain en fonction de la fréquence. D'une part, pour la plupart des systèmes, les deux phénomènes apparaissent pour des valeurs voisines de l'amortissement, d'autre part, si la réponse en fréquence est monotone (décroissante), le dépassement sera limité à quelques pour cent (5 % pour).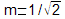

Le dessin ci-dessous illustre le raisonnement graphique :

5.2.b Marge de phase et marge de gain

Les coordonnées du point critique correspondent à un module égal à 1 (en échelle linéaire) et à une phase égale à 180°. La distance au point critique est classiquement repérée par deux grandeurs :

• La marge de phase, Df, est le déphasage supplémentaire qu'il faudrait rajouter au déphasage de la fonction de transfert en boucle ouverte, pour la fréquence à laquelle le gain vaut 1 (0dB), pour que son diagramme de Nyquist passe par le point critique.

• La marge de gain, DG, généralement comptée en décibels, est l'augmentation de gain (un coefficient multiplicateur) qu'il faudrait donner à la fonction de transfert, à la fréquence pour laquelle son déphasage vaut 180°, pour que le diagramme de Nyquist passe par le point critique.

La figure ci-dessous illustre ces définitions, et montre que l'on définit bien une « distance » au point critique.

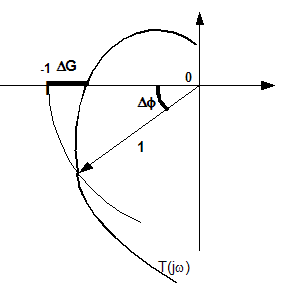
Typiquement, un amortissement idéal, la limite du dépassement dans la réponse transitoire, correspond à une marge de phase d'au moins 50 à 60° et une marge de gain d'au moins 6dB.

Les systèmes du second ordre n'ont pas de marge de gain, seule la marge de phase peut être définie.

5.2.c Analyse sur les diagrammes de Bode

Évidemment, tout ce qui vient d'être dit peut être transcrit sur les diagrammes de Bode. Sur le diagramme ci-dessous, on a repris l'exemple stable du retard intégrateur pour illustrer la définition des marges de gain et de phase.

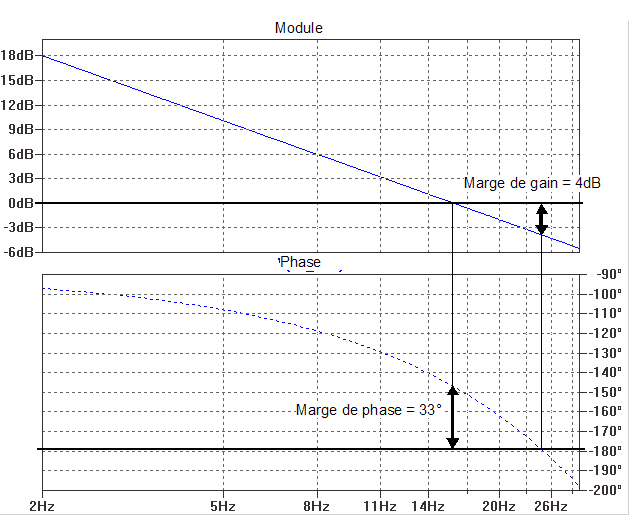
Les valeurs relativement faibles de ces marges correspondent à un réponse sous amortie, comme nous l'avons vu précédemment. Ces valeurs peuvent évidemment être retrouvées sur le diagramme de Nyquist du même système (voir plus haut).

L'intérêt des diagrammes de Bode est qu'ils sont d'une construction beaucoup plus simple que les diagrammes de Nyquist, et permettent de calculer « graphiquement » des correcteurs quand le résultat n'est pas satisfaisant.

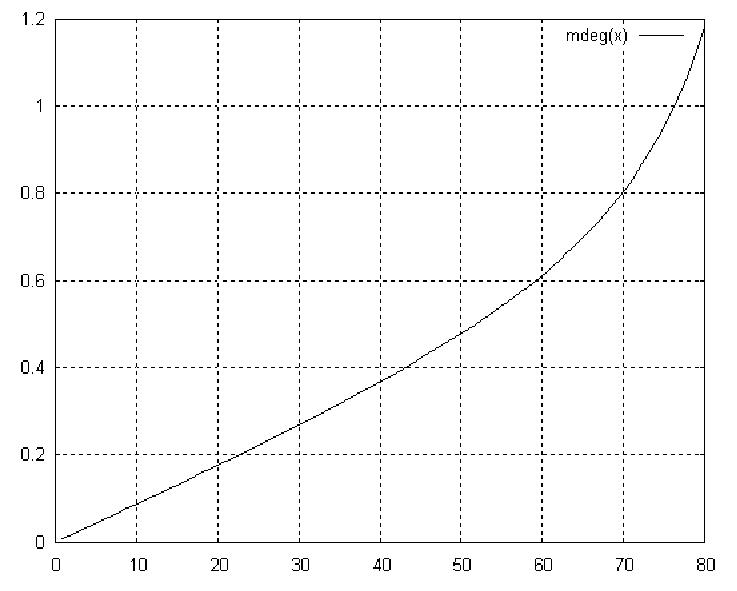
Marge de phase (en degrés) et amortissement pour un système du second ordre :