Avant de traiter des exemples de mises en équations de systèmes (électrique, mécanique, hydraulique et thermique), il faut prendre conscience des analogies qui existent dans les différents domaines de la physique. Dans le tableau ci-dessous sont présentées les grandeurs physiques analogues dans ces différents domaines.
| | Systèmes électriques | Systèmes mécaniques
en translation |
Systèmes mécaniques
en rotation | Systèmes hydrauliques | Systèmes thermiques | Systèmes optiques |
Les deux
grandeurs
de base | Courant
i(t) en A
Tension
u(t) en V |
Vitesse linéaire
v(t) en m/s
Force
f(t) en N | Vitesse angulaire
w(t) en rad/s
Couple
g(t) en N.m |
Débit
q(t) en m3/s
Pression
p(t) en Pa | Puissance
pu(t) en W
Température
q(t) en K |
Éclairement
e(t) en lx
Flux lumineux
f(t) en lm |
Intégrale
de la première
grandeur | §i.dt = q(t)
Charge élect.
en C (A.s) |
§v.dt = x(t)
Position
en m |
§w.dt = q (t)
Position ang.
en rad | §q.dt = v(t)
Volume
en m3 | §pu.dt = en(t)
Enthalgie
en J (W.s) | §e.dt = ex(t)
Exposition
en lx.s |
5.5.1 Exemple électrique
Soit le schéma ci-dessous (4 résistances et 3 capacités). La commande est la tension VE et la sortie la tension VS.
Remarque: on utilise les lettres majuscules pour signifier qu'on exprime les images des fonctions du temps.
Pour faire la mise en équations on introduit des variables internes (4 courants et 2 tensions).
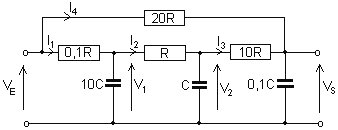 |
Les équations symboliques sont:
I1 = (VE - V1)/0,1R I2 = (V1 - V2)/R
I3 = (V2 - VS)/10R I4 = (VE - VS)/20R
V1 = (I1 - I2)/10Cp V2 = (I2 - I3)/Cp
VS = (I3 + I4)/0,1Cp |
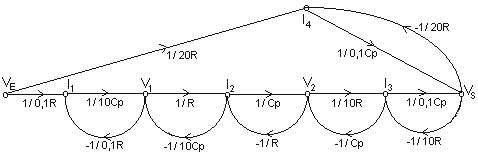
6 boucles et 2 chemins directs:
D = 1 + (1/ RCp)[1+0,1+1+0,1+1+0,5] + (1/ R2C2p2)[1+0,1+1+0,5+0,01+0,1+0,05+1+0,5+0,05] + (1/ R3C3p3)[1+0,5+0,05+0,005]
= 1 + 3,7/(RCp) + 4,31/(R2C2p2) + 1,555/(R3C3p3)
STkDk = 1/ R3C3p3 + (0,5/RCp)[1 + 2,2/(RCp) + 1,11/(R2C2p2)]
= 1,555/(R3C3p3) + 1,1/(R2C2p2) + 0,5/(RCp)
VS / VE = (1,555 + 1,1RCp + 0,5R2C2p2) / (1,555 + 4,3RCp + 3,7R2C2p2 + R3C3p3)
= (1 + 0,707RCp + 0,322R2C2p2) / (1 + 2,77RCp + 2,38R2C2p2 + 0,643R3C3p3)
Bien sûr on peut factoriser le dénominateur et de plus poser t = RC :
VS / VE = (1 + 0,707tp + 0,322t2p2) / (1 + 1,392tp)(1 + 0,802tp)(1 + 0,576tp)
5.5.2 Exemple mécanique
Soit le montage mécanique en translation ci-dessous (2 masses guidées suivant l'axe horizontal, 2 ressorts et 2 amortisseurs). La commande est la position X [image de x(t)] et la sortie la position Z [image de z(t)].
Pour faire la mise en équations on introduit des variables internes (2 résultantes de forces et une position).
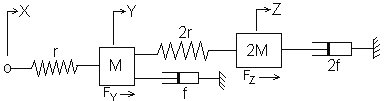 |
Les équations symboliques sont:
FY = rX + 2rZ - (3r + fp)Y
FZ = 2rY - 2(r + fp)Z
Y = FY / Mp2
Z = FZ / 2Mp2
|
Explications: un ressort transmet une force proportionnelle à la position relative de ses extrémités [exemple: r(X-Y)], alors qu'un amortisseur (frottement visqueux) transmet une force proportionnelle à la vitesse relative de déplacement de ses extrémités, donc à la dérivée de la position [exemple: -fpY]. La force est positive si elle va dans le sens de l'augmentation de la position, elle est négative si elle est opposée (force résistante).
Quand on a exprimé la résultante des forces qui s'exercent sur une masse, on divise par la valeur de cette masse et on obtient son accélération. Une intégration donne la vitesse, une seconde intégration donne la position.
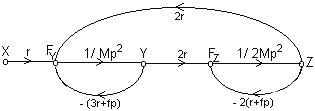
3 boucles et 1 chemin direct:
D = 1 + (3r+fp)/(Mp2) + (r+fp)/(Mp2) - 2r2/(M2p4) + (3r2+4rfp+f2p2)/(M2p4)
= [r2 + 4rfp + (f2+4rM)p2 + 2fMp3 + M2p4] / (M2p4)
STkDk = r2 / (M2p4)
Z / X = 1 / [1 + (4f/r)p + (f2/r2 + 4rM/r2)p2 + (2fM/r2)p3 + (M2/r2)p4]
A.N.: M = 1,2 kg ; r = 1 kg/s2 et f = 0,8 kg/s : Z / X = 1 / (1 + 3,2p +5,44p2 + 1,92p3 + 1,44p4)
Le dénominateur se factorise en 2 facteurs du second degré:
Z / X = 1 / [(1+2,986p+4,480p2)(1+0,214p+0,321p2)].
5.5.3 Exemple hydraulique
Soit le montage hydraulique ci-dessous constitué de 2 réservoirs et 3 tuyaux (résistances hydrauliques). La commande est le débit QE [image de qe(t)] et la sortie le niveau H [image de h(t)].
Pour faire la mise en équations on introduit des variables internes (3 débits et 1 niveau).
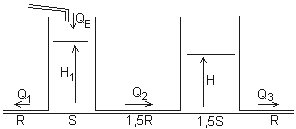 |
Les équations symboliques sont:
H1 = (QE - Q1 - Q2) / Sp
Q1 = H1 / R Q3 = H / R
Q2 = (H1 - H) / (1,5R)
H = (Q2 - Q3) / (1,5Sp)
|
Explications: on suppose que l'écoulement dans les tuyaux est "laminaire" et non "turbulent". Dans ces conditions le débit est proportionnel à la différence de pression, donc à la différence de niveau du liquide. Si le liquide est de l'eau, une hauteur de 1 m correspond à une pression de 104 Pa (1 cm d'eau = 1 hPa). La résistance hydraulique qui intervient dans les équations est donc le rapport entre une hauteur et un débit (elle s'exprime alors en s/m2). D'autre part un réservoir est un intégrateur de débit (le volume d'eau est l'intégrale de la résultante des débits). Pour avoir le niveau on divise le volume par la section. La section d'un réservoir est analogue à la capacité électrique d'un condensateur.
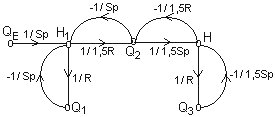
4 boucles et 1 chemin direct. On pose t = RS
D = 1 + (1/tp)[1+2/3+4/9+2/3] + (1/t2p2)[4/9+2/3+4/9] = (1/t2p2)[1,555 + 2,777tp + t2p2]
STkDk = (4R)/(9t2p2)
H / QE = (0,444R) / (1,555 + 2,777tp + t2p2) = (0,285R) / (1 + 1,785tp + 0,643t2p2) =
(0,285R) / [(1+1,284tp)(1+0,501tp].
5.5.4 Exemple thermique
Soit un gros transistor de puissance dont la jonction est chauffée par la puissance instantanée appliquée (tension x courant), et refroidie par les liaisons thermiques au boîtier, au radiateur et à l'air ambiant. Le montage comprend 4 résistances thermiques (jonction-boîtier, boîtier-radiateur, boîtier-air, radiateur-air) et 3 capacités thermiques (jonction, boîtier, radiateur).
La commande est la puissance PE dissipée dans la jonction [image de pE(t)] et la sortie est la température QB du boîtier [image de qB(t)].
Pour faire la mise en équations de ce système thermique nous allons faire un schéma électrique équivalent. La grandeur analogue de la puissance thermique sera un courant électrique et la température aura pour grandeur analogue une tension (différence de potentiel). La référence de température est ici l'air ambiant.
En plus de la commande et de la sortie, pour faire la mise en équations on introduit des variables internes (2 puissances thermiques et 2 températures)
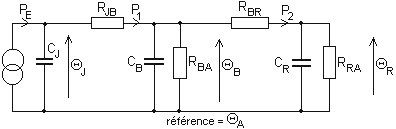
Les équations symboliques sont:
QJ = (PE - P1) / CJp |
P1 = (QJ - QB) / RJB |
QB = ZB(P1 - P2) |
P2 = (QB - QR) / RBR |
QR = ZR.P2 |
avec ZB = RBA / (1 + RBACBp) et
ZR = RRA / (1 + RRACRp) . La lettre A correspond bien sûr à "air ambiant".
Nous allons calculer la fonction de transfert QB / PE avec des applications numériques:
RJB = 0,75 K/W ; RBR = 0,2 K/W ; RBA = 4 K/W ; RRA = 1,2 K/W ; CJ = 1,5 J/K ; CB = 12 J/K ; CR = 60 J/K .
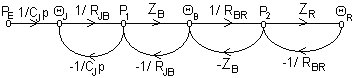
4 boucles et 1 chemin direct:
D = 1 + 0,888/p + 5,333/(1+48p) + 20/(1+48p) + 6/(1+72p) + 17,777/[p(1+48p)] + 5,333/[p(1+72p)] + 32/[(1+48p)(1+72p)]
= [p(1+120p+3456p2) + 0,888(1 + 120p + 3456p2) + 25,333p(1+72p) + 6p(1+72p) + 5,333(1+48p) + 32p] / [p(1+72p)(1+48p)]
= [24 + 1707p + 5304p2 + 3456p3] / [p(1+72p)(1+48p)]
STkDk =
3,555/[p(1+48p)].[1 + 6/(1+72p)] = [3,555(7+72p)][p(1+72p)(1+48p)]
QR / PE = [24,888 + 256p] / [24 + 1707p + 5304p2 + 3456p3] = 1,037[1 + 10,285p] / [1 + 71,125p + 221p2 + 144p3]
QR / PE = 1,037[1+10,285p] / [(1+69,03p)(1+2,30p)(1+0,92p)] .
Intéressons nous maintenant aussi à la température de la jonction puis à celle du radiateur.
Sortie: QJ
STkDk =
(0,666/p).[1 + 5,333/(1+48p) + 20/(1+48p) + 6/(1+72p) + 32/(1+48p)(1+72p)]
= [0,666(64,333 + 2232p + 3456p2] / [p(1+72p)(1+48p)]
QJ / PE = [42,888 + 1488p + 2304p2] / [24 + 1707p + 5304p2 + 3456p3]
QJ / PE = 1,787[1+33,11p)(1+1,62p)] / [(1+69,03p)(1+2,30p)(1+0,92p)] .
Sortie: QR
STkDk = 21,333 / [p(1+72p)(1+48p)]
QR / PE = [21,333] / [24 + 1707p + 5304p2 + 3456p3]
QR / PE = 0,888 / [(1+69,03p)(1+2,30p)(1+0,92p)]
Pour une température ambiante de 23 °C et une puissance dissipée dans la jonction de 70 W, au bout d'environ 7 minutes (la plus grande constante de temps est de 69 s), les températures se stabilisent à:
qJ = 1,787x70 + 23 = 148,1 °C
qB = 1,037x70 + 23 = 95,6 °C
qR = 0,888x70 + 23 = 85,1 °C
Fin du chapitre 5
Dans le chapitre 6 nous allons (enfin !) aborder l'étude des systèmes bouclés, donc des asservissements.

