Nous avons vu au chapitre 2 (2.10) qu'une fonction de transfert quelconque d'ordre n pouvait se mettre sous la forme:

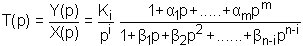
Nous allons étudier la fonction de transfert d'ordre 4, la généralisation à l'ordre n ne pose aucune difficulté. Il sera toujours facile de mettre en facteur, au dénominateur de la fonction de transfert, le coefficient du terme de plus haut degré en p. Pour notre application à l'ordre 4 il faut mettre la fonction de transfert sous la forme:
T(p) = Y/X = [a₀ + a₁p + a₂p² + a₃p³ + a₄p⁴] / [b₀ + b₁p + b₂p² + b₃p³ + p⁴]
Le coefficient en p⁴ au dénominateur est égal à 1.
Si b₀ = 0  T(p) est de classe 1, si de plus b₁ = 0  T(p) est de classe 2.
Ci-dessous sont présentés les deux graphes canoniques. L'utilisation de la règle de Mason permet de montrer que ces deux graphes ont une fonction de transfert Y/X conforme à celle ci-dessus. Vérifiez vous-même à titre d'exercice (4 boucles, aucune disjointe, 5 chemins directs). Le résultat est très vite obtenu.

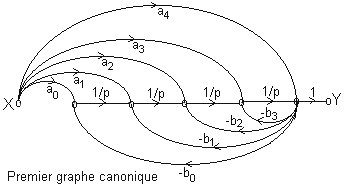
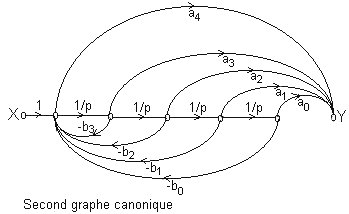
Remarque: le plus souvent le degré m du numérateur de la fonction de transfert est inférieur au degré n du dénominateur. Ici on aurait a₄ = 0.

Ces graphes canoniques montrent que toute fonction de transfert peut être simulée grâce aux composants suivants: intégrateurs, gains, sommateurs.
Avant les ordinateurs, il existait des calculateurs analogiques utilisant cette technique.
Pour être plus concret nous allons faire une application complète: à partir de l'expression d'une fonction de transfert d'ordre 4, déterminer un schéma de simulation avec un réglage indépendant de chaque paramètre.

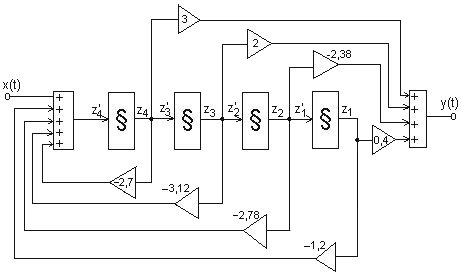
Soit la fonction de transfert Y/X = [0,8 - 4,76p + 4p² + 6p³] / [ 2,4 + 5,56p + 6,24p² + 5,4p³ + 2p⁴].
La première chose à faire est de diviser le numérateur et le dénominateur par 2 (pour avoir p⁴ au dénominateur):
Y/X = [0,4 - 2,38p + 2p² + 3p³] / [ 1,2 + 2,78p + 3,12p² + 2,7p³ + p⁴].

Le premier graphe canonique est donc:

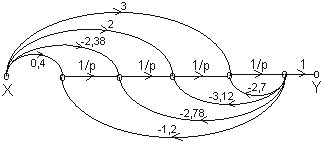
On peut ainsi matérialiser ce système avec 4 intégrateurs, 8 gains (réglage indépendant de chaque coefficient), et 4 sommateurs à 3 entrées:

Il est très facile de réaliser ce schéma sur un calculateur analogique ou sur un simulateur de fonctions de transfert.
Bien sûr le système qui renferme le symbole § est un intégrateur.
On peut même imposer des conditions initiales non nulles (sur chaque intégrateur) avant d'appliquer l'entrée x(t). 
 
Nous avons introduit des variables internes z_k qui seront utiles pour présenter le paragraphe suivant.

Le second graphe canonique est:

On peut cette fois matérialiser ce système avec 4 intégrateurs, 8 gains et 2 sommateurs à 5 entrées: (voir page suivante).
Les variables internes z_k ne sont évidemment pas les mêmes que dans le schéma précédent.