Nous allons étudier ces représentations grâce à l'exemple d'ordre 4 vu au paragraphe 5.3. 
 
Première représentation d'état (voir au paragraphe 5.3 le schéma de matérialisation issu du premier graphe canonique).

On a donné un nom à la sortie de chaque intégrateur: z_k(t).
Le système étant d'ordre 4 on a 4 variables internes qui constituent ce qu'on appellera un « vecteur d'état ». 
 
L'entrée d'un intégrateur correspond à la dérivée de sa sortie. Ainsi à partir du schéma on peut écrire:

z'₁ = - 1,2.z₄ + 0,4.x     z'₂ = z₁ - 2,78.z₄ - 2,38.x     z'₃ = z₂ - 3,12.z₄ + 2.x     z'₄ = z₃ - 2,7.z₄ + 3.x      y = z₄ .

Deuxième représentation d'état (voir le schéma de matérialisation issu du second graphe canonique au paragraphe 5.3). Bien sûr on a pris les mêmes notations pour les variables internes (variables d'état), mais elles ne sont pas les mêmes que précédemment. Ici on peut écrire:

z'₁ = z₂     z'₂ = z₃     z'₃ = z₄     z'₄ = - 1,2.z₁ - 2,78.z₂ - 3,12.z₃ - 2,7.z₄ + x
y = 0,4.z₁ - 2,38.z₂ + 2.z₃ + 3.z₄ .

Ci-dessous sont données les deux représentations d'état (vecto-matricielle).

Première représentation d'état: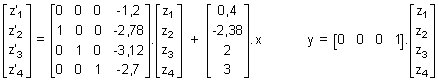

Seconde représentation d'état: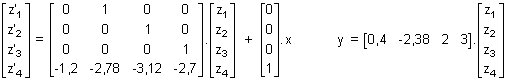

Généralisation:
On peut représenter le fonctionnement d'un système linéaire d'ordre n par deux équations vecto-matricielles en introduisant un vecteur d'état z à n composantes:

avec  A = matrice d'état (n lignes, n colonnes)   B = matrice d'entrée (n lignes, 1 colonne)   C = matrice de sortie (1 ligne, n colonnes). 
 

Soit T(p) la fonction de transfert générale d'un processus avec bn = 1:
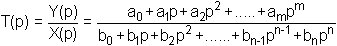Première représentation d'état:	Seconde représentation d'état:

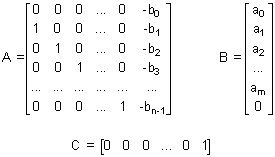La résolution du système de deux équations vecto-matricielles consiste à diagonaliser la matrice d'état. Le logiciel Matlab effectue ce travail en une toute petite fraction de seconde !