Nous allons étudier la réponse des systèmes élémentaires à un échelon de commande: x(t) = u(t)
[Lu(t) = 1/p].
Ainsi YIND(p) = T(p).1/p = YIMP(p).1/p .
On constate donc que pour n'importe quel système, donc pour T(p) quelconque, la réponse indicielle est l'intégrale de la réponse impulsionnelle. Inversement la réponse impulsionnelle est la dérivée de la réponse indicielle:
yimp(t) = dyind(t)/dt et yind(t) = §yimp(t).dt .
Afin d'être plus proche de l'expérimentation, nous étudierons les réponses non pas à un échelon-unité, mais à un échelon de commande d'amplitude a: x(t) = a.u(t) [X(p) = a/p].
3.3.1 Dérivateur
T(p) = p d'où: YIND(p) = p.a/p = a donc: yind(t) = a.d(t).
C'est une impulsion de Dirac de surface a.
3.3.2 Intégrateur
T(p) = 1/p d'où: YIND(p) = 1/p.a/p = a/p2 donc: yind(t) = a.t.u(t).
C'est une rampe de pente a (rampe de position), donc un échelon de vitesse de a unités par seconde.
Nous savions déjà que pour générer une rampe il suffit d'intégrer un échelon.
3.3.3 Premier ordre
T(p) = Y/X = A/(1+ tp) d'où:
YIND(p) = [A/(1+ tp)].a/p = aA/[p(1+tp)]
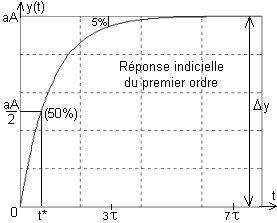
donc: yind(t) = aA(1-e-t/t)u(t). C'est une courbe exponentielle qui, à partir de la valeur initiale, varie de Dy = a.A où a représente l'amplitude de l'échelon et A le gain en position (gain statique) du système.
Au paragraphe 3.2.3 nous avons déterminé les temps correspondants à des valeurs particulières de l'exponentielle e-t/t.
Ainsi nous savons que le régime permanent est atteint au bout d'un temps tµ = 7t , que le temps de réponse à 5% vaut tR5% = 3t , et enfin que le temps à 50% de la variation est t*= t.ln2 .
|
yind(t) = aA(1-e-t/t)u(t)
|
Identification: il s'agit grâce à cet enregistrement de retrouver la fonction de transfert T(p) c'est-à-dire ici les valeurs de A et t:
A = Dy/Dx = Dy/a t = t*/ln2 @ 1,44t*.
La mesure de t* à 50% de la variation est précise et commode.
La mesure de tR5% est très peu précise car la pente de la courbe est faible. |
Formule de Bureau:
Si la constante de temps est grande (cas des systèmes thermiques et hydrauliques), il faut beaucoup de temps pour atteindre la valeur finale. Or, si nous ne connaissons pas cette valeur finale nous ne pouvons pas identifier le système. La formule de Bureau permet de déterminer cette valeur finale yµ en n'ayant enregistré qu'une partie de la réponse. Ce temps d'enregistrement sera alors divisé en 2, ainsi nous pourrons mesurer la valeur de y pour un temps T1: y1 = y(T1) , et pour un temps 2T1: y2 = y(2T1).
y1 = yµ(1-e-T1/t) et y2 = yµ(1-e-2T1/t)
y12 = yµ2(1-e-T1/t)2 = yµ2(1 -2e-T1/t + e-2T1/t)
2y1-y2 = yµ(1 -2e-T1/t + e-2T1/t) Le rapport y12/(2y1-y2) donne yµ.
|
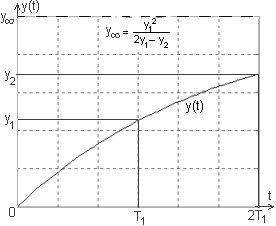 |
Attention: les valeurs y1, y2 et yµ doivent être déterminées par rapport à la valeur initiale (ici supposée nulle).
3.3.4 Second ordre
T(p) = Y/X = B/(1+2zp/w0 + p2/w02) d'où
Y(p) = aB/[p(1+2zp/w0 + p2/w02)]
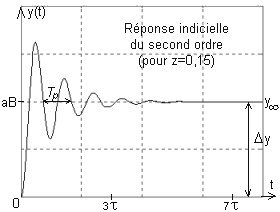
donc: yind(t) = aB[1 - b.e-t/t.sin(wpt + f)]u(t).
C'est une sinusoļde amortie dans une enveloppe exponentielle qui, à partir de la valeur initiale, varie en régime établi de Dy = a.B où a représente l'amplitude de l'échelon et B le gain en position (gain statique) du système,
avec b = (1-z2)-1/2 , wp = w0(1-z2)1/2 = pulsation propre
f = arc cos z
et t = 1/zw0 = constante de temps de l'enveloppe.
Temps de réponse à 5%: tR5% = 3t.
Durée totale du régime transitoire: tµ = 7t.
Pseudo-période propre de la sinusoļde: Tp = 2p/wp.
|
yind(t) = aB[1-b.e-t/t.sin(wpt + f)]u(t)
 |
Calcul du maximum de yind(t):
Le maximum correspond à l'annulation de la dérivée de yind(t), c.à.d. de yimp(t). En se reportant au paragraphe 3.2.4 on sait que: |
yimp(t) = 0 pour tm = Tp /2 = p/wp, donc pour wp.tm = p.
Dans l'expression de ymax apparaît sin(p + f) = -sin f .
Or cos f = z .
D'où: -sin f = -(1-z2)1/2 = -1/b.
Il y a une simplification: b.sin f = 1. Il vient:
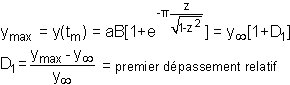
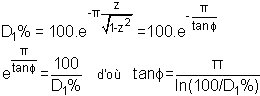 avec cosf = z avec cosf = z | 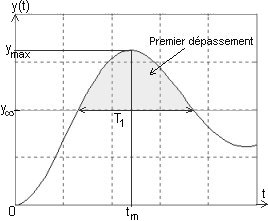 |
| Le temps de montée et le temps de premier dépassement sont égaux (une demi pseudo-période): tm = T1 = Tp /2 = p/wp.
|
Identification: les mesures de Dy, de D1% et de T1 permettent l'identification du système (détermination de la valeur des 3 paramètres B, z et w0). Pour le gain statique: B = Dy/Dx = Dy/a . Pour z et w0:
Exemple d'identification: on applique un échelon de commande de 2 unités. On mesure une variation Dy = 3 unités, un premier dépassement de 30% et un temps de montée de 0,75 s. Il vient: B = 3/2 = 1,5 . Les formules en bas de la page précédente donnent: z = 0,358 et w0 = 4,48 rad/s.
La fonction de transfert du système est donc T(p) = Y/X = 1,5/(1 + 0,16p + 0,05p2).
D'autre part les extréma de la fonction yind(t) se produisent périodiquement pour t = k.p/wp.
Ainsi les dépassements successifs s'expriment simplement en fonction du premier:
| Dk| = D1k (en valeur absolue car les dépassements impairs sont au-dessus de la valeur finale et sont donc positifs, alors que les dépassements pairs sont en dessous, donc négatifs). A.N.:
z = 0,15 : D1=62,1% D2=38,5% D3=23,9% D4=14,8% D5=9,2% D6=5,7% D7=3,5% D8=2,2%
D9=1,4% D10=0,8%
z = 0,30 : D1=37,2% D2=13,8% D3=5,1% D4=1,9% D5=0,7%
z = 0,45 : D1=20,5% D2=4,2% D3=0,8%
z = 0,60 : D1=9,5% D2=0,9%
z = 0,75 : D1=2,8% D2=0,0%
On peut donc, grâce à ces exemples, discuter de l'amortissement du système du second ordre en fonction de la valeur de z:
|
Pour z = 0,15 il y a 9 rebondissements supérieurs à 1% avant que la réponse ne se stabilise: l'amortissement est très faible.
Pour z = 0,30 il y a encore 4 rebondissements: l'amortissement est faible.
Pour z = 0,45 il n'y a plus que 2 rebondissements: l'amortissement est acceptable.
Pour z = 0,60 il n'y a qu'un seul rebondissement (de l'ordre de 10%): l'amortissement est bon.
Pour z = 0,75 le premier dépassement est inférieur à 3 %: l'amortissement est fort.
Pour des valeurs de z supérieures à 0,75 la réponse est presque comparable à celle d'un second ordre apériodique (très fort amortissement).
La relation qui donne le temps de montée (en bas de la page précédente) montre que celui-ci augmente avec z. Il y a donc un compromis entre la vélocité du système et son amortissement.
On essayera toujours que la réponse indicielle d'un asservissement soit comparable à celle d'un second ordre bien amorti (z de l'ordre de 0,5). Pour z = 0,5 on a D1=16,3%. |
|

