L'impulsion de Dirac est définie mathématiquement comme étant la dérivée d'un échelon unité parfait. Ce serait donc une impulsion (à l'instant t=0) d'amplitude infinie et de largeur nulle, dont la surface serait 1. Cette impulsion de Dirac est notée d(t).
L'image de l'échelon unité étant 1/p et la fonction de transfert du dérivateur étant p, on en déduit:
Ld(t) = 1.
C'est l'unique fonction du temps dont l'image ne dépend pas de la variable symbolique p. Malheureusement cette fonction ne peut pas être réalisée en pratique.
Aussi puisque l'image de l'impulsion de Dirac est égale à 1, YIMP(p) = T(p) pour n'importe quel système.
L'image de la réponse impulsionnelle d'un système quelconque s'identifie à sa fonction de transfert.
Donc la réponse impulsionnelle est la fonction du temps « originale » de T(p): yimp(t) = L-1T(p).
3.2.1 Dérivateur: y(t) = dx(t)/dt
La réponse impulsionnelle du dérivateur n'est pas définie.
3.2.2 Intégrateur: y(t) = §x(t)dt
T(p) = Y/X = 1/p yimp(t) = u(t).
La réponse impulsionnelle de l'intégrateur est l'échelon unité.
|
3.2.3 Premier ordre: t.dy(t)/dt + y(t) = A.x(t)
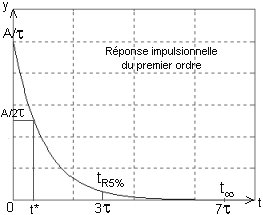
T(p) = Y/X = A/(1+ tp) yimp(t) = A/t.e-t/t.u(t) C'est une impulsion exponentielle.
Pour t = 0 e-t/t = 1 = 100%.
Calculons le temps ta tel que e-ta/t = a/100 :
eta/t = 100/a d'où ta = t.ln(100/a).
A.N.: a = 50% t* = t.ln2
a = 36,8% t @ t
a = 5% tR5% = 3t
a = 1% tR1% = 5t
a < 0,1% tµ = 7t
|
yimp(t) = A/t.e-t/t.u(t)
 |
|
3.2.4 Second ordre: b.d2y(t)/dt2 + a.dy(t)/dt + y(t) = B.x(t)
T(p) = B/(1+ap+bp2) On pose a =2z/w0 et b=1/w02
w0 = b-1/2 = pulsation naturelle et z = 0,5a. b-1/2 = coefficient d'amortissement.
T(p) = B/(1+2zp/w0 + p2/w02)
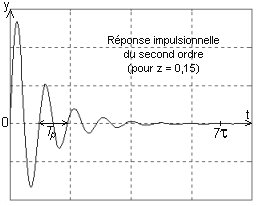
Si z<1 on a: yimp(t) = C.e-t/t.sin(wpt).u(t) C'est une sinusoļde amortie dans une enveloppe exponentielle.
avec C = B.wp /(1-z2) , wp = w0(1-z2)1/2 = pulsation propre
et t = 1/zw0 = constante de temps de l'enveloppe.
Au bout d'un temps tµ = 7t y(t) peut être considérée comme nulle.
|
yimp(t) = C.e-t/t.sin(wpt).u(t)
 |
La pseudo-période propre de la sinusoļde est: Tp = 2p/wp .
Le maximum de cette fonction est: ymax = B.w0.d.e-0,5pzd avec d= (1-z2)-1/2 .
Si z est supérieur ou égal à 1 on peut factoriser le dénominateur en deux facteurs du premier degré. Dans ce cas la réponse du système est simplement une somme de deux réponses du premier ordre. Les deux constantes de temps sont alors:
Si le coefficient d'amortissement z est inférieur à 1 le système est un second ordre élémentaire, on dit : système du second ordre pseudo-périodique.
Si z est supérieur ou égal à 1 ce n'est pas un second ordre élémentaire car on peut le décomposer en deux systèmes du premier ordre, on dit : système du second ordre apériodique.

