Nous allons calculer (ce sera très facile) les images de trois fonctions très utilisées en asservissement :  l'échelon de position, l'échelon de vitesse et l'échelon d'accélération (en Automatique on utilise une terminologie de mécanicien car les premiers asservissements industriels réalisés furent de technologie entièrement mécanique comme par exemple le régulateur de vitesse à boules sur les machines à vapeur).
Commençons par l'échelon-unité c.à.d. un échelon de une unité. Cette fonction sera nommée u(t). Elle est initialement nulle, et vaut 1 pour t > 0.
                          

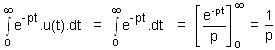
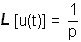
Si l'échelon a une amplitude de a unités alors son image est multipliée par a.
Si on intègre cet échelon on obtient la fonction  a.t.u(t)  qu'on appelle échelon de vitesse de a unités par seconde. La représentation de cette fonction est une rampe (de position) de pente a. Puisque cette fonction est l'intégrale de la précédente, son image est multipliée par 1/p.
Si on intègre une seconde fois on obtient la fonction a.t²/2 qu'on appelle un échelon d'accélération de a unités par seconde-carré. La représentation de cette fonction est une parabole (de position). Puisque cette fonction est l'intégrale de la précédente, son image est à nouveau multipliée par 1/p. Donc: