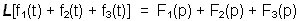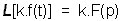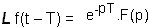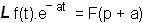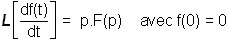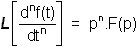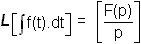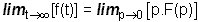Pour l'étude de la précision des asservissements on ne s'intéresse qu'à la valeur finale de la grandeur asservie. Nous verrons alors qu'il sera très simple de déterminer la valeur finale de cette fonction du temps sans connaître l'expression de cette fonction mais seulement son image.
La démonstration se fait en repartant de l'image de la dérivée g(t) d'une fonction
f(t) :

Cette dernière relation est utile pour connaître la valeur initiale ā t = 0+ uniquement s'il y a discontinuīté (c'est le cas par exemple de la réponse impulsionnelle d'un système du premier ordre). Sinon on trouvera toujours une valeur initiale nulle, c'est notre hypothèse de travail (voir paragraphe 2.3).
La seule relation qui nous intéresse vraiment est celle qui permet de déterminer la valeur finale de f(t):
Bien entendu dans la plupart des applications lorsqu'on multiplie F(p) par p il apparaît une simplification par p (sinon en faisant tendre p vers 0 le résultat serait toujours nul).
Nous en avons terminé avec les propriétés de la Transformée de Laplace. Elles sont au nombre de 8 et il est souhaitable de les apprendre par cur. Voici un récapitulatif :