L'hypothèse linéaire conduit en
régime établi à une sortie sinusoïdale de même fréquence. La sortie est
caractérisée par rapport à l'entrée avec un rapport en amplitude A et
une phase F.
Le calcul de
A et
F se fait directement en remplaçant
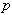
par
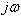
dans
la fonction de transfert
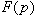
:
- Amplitude :
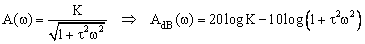
- Phase
:
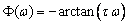
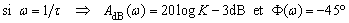
(pulsation de brisure)
- Réponse harmonique avec
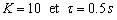 :
:

avec
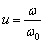
(pulsation réduite)
- Maximum en amplitude
(surtension) :
Si
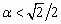
,
il existe un maximum pour
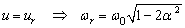
(pulsation
de résonance)
- Phase : si
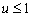 alors
alors 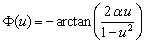
si
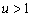
alors

·

- Réponse harmonique
avec
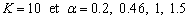 :
:
- Evolution de la surtension en
fonction du coefficient d'amortissement pour
 :
:
Dans les paragraphes 2.3.1 et 2.3.2, seuls des transferts stables (

)
ont été présentés. Nous évoquerons au chapitre suivant la propriété de
stabilité.
Pour compléter ces originaux, l’analyse
de l’influence de(s) zéro(s) dans les transferts peut être un exercice
intéressant. Nous pouvons citer au passage deux transferts particuliers qui
sont l’intégrateur et le dérivateur.

