Le fonctionnement d'un système linéaire compliqué, dont l'entrée de commande est x(t) et la sortie observée est y(t), peut être décrit par une équation différentielle linéaire à coefficients constants d'ordre n:
bny(n) + bn-1y(n-1) + bn-2y(n-2) + ........ + b2y'' + b1y' + b0y = amx(m) + am-1x(m-1) + ....... + a2x'' + a1x' + a0x
avec y(n) = dyn / dtn et m inférieur (ou au plus égal) à n.
La résolution de cette équation différentielle, pour une commande connue x(t) et un état initial connu, est un travail de Titan! En effet il faut d'abord rechercher une solution générale sans second membre (et pour une équation différentielle d'ordre élevé ce n'est pas de la tarte), puis trouver une solution particulière avec le second membre (alors là il faut du pif) et pour finir déterminer toutes les constantes d'intégration pour satisfaire aux conditions initiales!!!
Vous allez voir que dans le monde symbolique tout est très simple. Prenons l'image de cette équation différentielle.
On pose Y = L y et X = L x .
Nous savons que l'image de la dérivée nième de y est simplement pnY:
bnpnY + bn-1pn-1Y + bn-2pn-2Y + ........ + b2p2Y + b1pY + b0Y = ampmX + am-1pm-1X +....... + a2p2X + a1pX + a0X
Nous pouvons mettre Y en facteur dans le premier membre et X dans le second:
(bnpn + bn-1pn-1 + bn-2pn-2 + ........ + b2p2 + b1p + b0)Y = (ampm + am-1pm-1 +....... + a2p2 + a1p + a0)X
Il est donc excessivement simple d'exprimer Y en fonction de X:
Y = T(p).X où T(p) qu'on appelle Fonction de Transfert est un rapport de deux polynômes en p. Le polynôme du dénominateur de T(p) est du nième degré ce qui correspond à l'ordre n de l'équation différentielle:
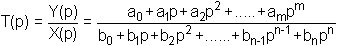
Mise de T(p) sous forme canonique:
Si b0 n'est pas nul, le système est dit de classe 0 et la forme canonique de T(p) est:
avec K0 = a0/b0 = gain en position (gain statique), ak = ak/a0 et bk = bk/b0.
Si b0 = 0 et si b1 est non nul, le système est dit de classe 1 (un intégrateur) et la forme canonique de T(p) est:
avec K1 = a0/b1 = gain en vitesse, ak = ak/a0 et bk = bk+1/b1.
Si b0 = 0 et si b1 = 0, le système est dit de classe 2 (deux intégrateurs) et la forme canonique de T(p) est:
avec K2 = a0/b2 = gain en accélération, ak = ak/a0 et bk = bk+2/b2.

